题目内容

如图所示，劲度系数k=20.0N/m的轻质水平弹簧右端固定在足够长的水平桌面上，左端系一质量为M=2.0kg的小物体A，A左边所系轻细线绕过轻质光滑的定滑轮后与轻挂钩相连。小物块A与桌面的动摩擦因数μ=0.15，设最大静摩擦力等于滑动摩擦力。现将一质量m=1.0kg的物体B挂在挂钩上并用手托住，使滑轮右边的轻绳恰好水平伸直，此时弹簧处在自由伸长状态。释放物体B后系统开始运动，取g=10m/s2。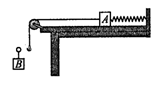

（1）求刚释放时物体B的加速度a；
（2）求小物块A速度达到最大时弹簧的伸长量x1；
（3）已知弹簧弹性势能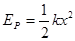，x为弹簧形变量，求整个过程中小物体A克服摩擦力年做的总功W。

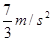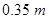（1）（2）（3）2.4 J

解析试题分析：（1） 对A、B两物体组成的系统由于mg＞μMg，所以B刚释放时物体A将开始向左运动，
此时弹簧弹力为零，据牛顿第二定律有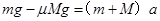：            （3分）
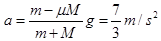解得                                    （2分）
（2） 在A向左加速过程中位移为x时A和B的加速度为a，
据牛顿第二定律有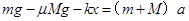                    （2分）
A第1次向左运动到a=0位置时，速度达到最大，设A此时向左运动位移为x1，则有： mg- μMg- kx1= 0                                              
解得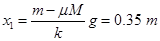        （2分）
（3）设A向左运动的最大位移为x2，则有mgx2= 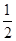kx22+μMgx2          （2分）
解得x2="0.7" m                                                （1分）
此时kx2＞mg+μMg，故A将向右运动。                          （1分）
设A向右运动返回到离初始位置距离为x3时速度再次减为零，则有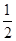
kx22- 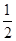kx32=mg（x2-x3）+μMg（x2-x3）                             （1分）
解得x3="0.6" m                                                  （1分）
此时mg＜μMg+kx3，所以A静止在x3处。                         （1分）
整个过程中A运动的总路程s=x2+（x2-x3）="0.8" m                    （1分）
A克服摩擦力所做总功W="μMgs=2.4" J                             （1分）
考点：考查了牛顿第二定律，能量守恒定律的综合应用

练习册系列答案
相关题目

若两颗人造地球卫星的周期之比为T1∶T2＝2∶1，则它们的轨道半径之比R1∶R2＝＿＿＿＿，向心加速度之比a1∶a2＝＿＿＿＿。

（12分）如图所示，质量为m=1kg可看作质点的小球以一定初速度沿桌子边缘水平飞出，下落高度h=0.8m后恰好沿A点的切线方向进入竖直放置的半径R=1m的光滑圆轨道ABC，空气阻力不计，取g=10m/s2，sin53°=0.8，求：

（1）小球运动到A点时速度的大小
（2）小球对轨道B点的压力

（16分）光滑圆轨道和两倾斜直轨道组成如图所示装置，其中直轨道bc粗糙，直轨道cd光滑，两轨道相接处为一很小的圆弧。质量为m=0.1kg的滑块（可视为质点）在圆轨道上做圆周运动，到达轨道最高点a时的速度大小为v=4m/s，当滑块运动到圆轨道与直轨道bc的相切处b时，脱离圆轨道开始沿倾斜直轨道bc滑行，到达轨道cd上的d点时速度为零。若滑块变换轨道瞬间的能量损失可忽略不计，已知圆轨道的半径为R=0.25m，直轨道bc的倾角θ=37o，其长度为L=26.25m，d点与水平地面间的高度差为h=0.2m，取重力加速度g=10m/s2，sin37°=0.6。求：

（1）滑块在圆轨道最高点a时对轨道的压力大小；
（2）滑块与直轨道bc问的动摩擦因数；

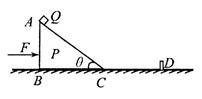
（16分）如图所示，水平地面上静止放置一辆小车A，质量，上表面光滑，小车与地面间的摩擦力极小，可以忽略不计。可视为质点的物块B置于A的最右端，B的质量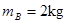。现对A施加一个水平向右的恒力F＝10N，A运动一段时间后，小车左端固定的挡板B发生碰撞，碰撞时间极短，碰后A、B粘合在一起，共同在F的作用下继续运动，碰撞后经时间t＝0.6s，二者的速度达到。求

（1）A开始运动时加速度a的大小；
（2）A、B碰撞后瞬间的共同速度v的大小；
（3）A的上表面长度l；

（20分）如图所示，在光滑的水平面上有一质量为m=1kg的足够长的木板C，在C上放置有A、B两物体，A的质量mA=1kg，B的质量为mB=2kg．A、B之间锁定一被压缩了的轻弹簧，弹簧储存的弹性势能Ep=3J，现突然给A、B一瞬时冲量作用，使A、B同时获得v0=2m/s的初速度，且同时弹簧由于受到扰动而解除锁定，并在极短的时间内恢复原长，之后与A、B分离．已知A和C之间的摩擦因数为μ1=0.2，B、C之间的动摩擦因数为μ2=0.1，且滑动摩擦力略小于最大静摩擦力．求：

（1）弹簧与A、B分离的瞬间，A、B的速度分别是多大？
（2）已知在C第一次碰到右边的固定挡板之前，A、B和C已经达到了共同速度，求在到达共同速度之前A、B、C的加速度分别是多大及该过程中产生的内能为多少？
（3）已知C与挡板的碰撞的碰撞无机械能损失，求在第一次碰撞后到第二次碰撞前A在C上滑行的距离？

（20分）如图甲所示，间距为d、垂直于纸面的两平行板P、Q间存在匀强磁场。取垂直于纸面向里为磁场的正方向，磁感应强度随时间的变化规律如图乙所示。t=0时刻，一质量为m、带电荷量为+q的粒子（不计重力），以初速度由板左端靠近板面的位置，沿垂直于磁场且平行于板面的方向射入磁场区。当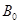和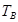取某些特定值时，可使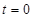时刻入射的粒子经时间恰能垂直打在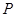板上（不考虑粒子反弹）。上述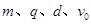为已知量。

（1）若，求；
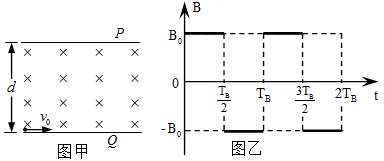
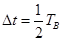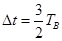（2）若，求粒子在磁场中运动时加速度的大小；  
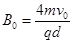（3） 若，为使粒子仍能垂直打在板上，求。

如图所示，水平地面上有一个静止的直角三角滑块P，顶点A到地面的距离h=1.8m，水平地面上D处有一固定障碍物，滑块的C端到D的距离L=6．4m。在其顶点么处放一个小物块Q，不粘连，最初系统静止不动。现在滑块左端施加水平向右的推力F=35N，使二者相对静止一起向右运动，当C端撞到障碍物时立即撤去力F，且滑块P立即以原速率反弹，小物块Q最终落在地面上。滑块P的质量M=4．0kg，小物块Q的质量m=1．0kg，P与地面间的动摩擦因数。（取g=10m／s2）求：

（1）小物块Q落地前瞬间的速度；
（2）小物块Q落地时到滑块P的B端的距离。

（8分）一同学在a=2m/s2匀加速下降的升降机中最多能举起m1=75kg的物体。取g=10m/s2，求：
（1）此人在地面上可举起物体的最大质量；
（2）若该同学在一匀加速上升的升降机中最多能举起m2=50kg的物体，则该升降机上升的加速度为多大？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网