题目内容
如图所示,质量M=0.01kg的导体棒ab,垂直放在相距l=0.1m的平行光滑金属导轨上.导轨平面与水平面的夹角θ=30°,并处于磁感应强度大小B=5T、方向垂直于导轨平面向下的匀强磁场中.左侧是水平放置的平行金属板,它的极板长s=0.1m,板间距离d=0.01m.定值电阻R=2Ω,Rx为滑动变阻器的阻值,不计其它电阻.
(1)调节Rx=2Ω,释放导体棒,当棒沿导轨匀速下滑时,求通过棒的电流I及棒的速率v;
(2)改变Rx,待棒沿导轨再次匀速下滑后,将质量m=10-8kg、电量q=10-4C的带正电的粒子从两金属板中央左侧以v0=103m/s水平射入,(不计粒子的重力),若它恰能从下板右边缘射出,求此时的Rx.
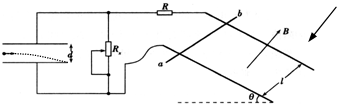
(1)调节Rx=2Ω,释放导体棒,当棒沿导轨匀速下滑时,求通过棒的电流I及棒的速率v;
(2)改变Rx,待棒沿导轨再次匀速下滑后,将质量m=10-8kg、电量q=10-4C的带正电的粒子从两金属板中央左侧以v0=103m/s水平射入,(不计粒子的重力),若它恰能从下板右边缘射出,求此时的Rx.

分析:由电磁感应定律求电动势E=BLv、闭合电路欧姆定律求电流I=
,由导体棒受力平衡求速度,由带电粒子的匀速通过电容器求电压,结合闭合电路求速度.
| E |
| R |
解答:解:(1)导体棒匀速下滑时,Mgsinθ=BIl①
I=
②
将数据代入上式,即可解得:I=
A=0.1A
设导体棒产生的感应电动势为E0
E0=Blv③
由闭合电路欧姆定律得:
I=
④
联立②③④,得
v=
=
=0.8m/s;
(2)改变Rx由②式可知电流不变.它恰能从下板右边缘射出,
则有:
=
at2⑥
而a=
⑦
且t=
⑧
联立⑥⑦⑧,得:U=1V;
根据RX=
,可解得:Rx=
Ω=10Ω;
答:(1)通过棒的电流0.1A及棒的速率0.8m/s;
(2)若它恰能从下板右边缘射出,则此时的Rx为10Ω.
I=
| Mgsinθ |
| B l |
将数据代入上式,即可解得:I=
0.01×10×
| ||
| 5×0.1 |
设导体棒产生的感应电动势为E0
E0=Blv③
由闭合电路欧姆定律得:
I=
| E0 |
| R+RX |
联立②③④,得
v=
| I(R+RX) |
| B l |
| 0.1×(2+2) |
| 5×0.1 |
(2)改变Rx由②式可知电流不变.它恰能从下板右边缘射出,
则有:
| d |
| 2 |
| 1 |
| 2 |
而a=
| qU |
| md |
且t=
| s |
| v0 |
联立⑥⑦⑧,得:U=1V;
根据RX=
| U |
| I |
| 1 |
| 0.1 |
答:(1)通过棒的电流0.1A及棒的速率0.8m/s;
(2)若它恰能从下板右边缘射出,则此时的Rx为10Ω.
点评:考查了电磁感应定律与闭合电路欧姆定律的应用,掌握牛顿第二定律与运动学公式的综合运用,注意粒子恰好从下边缘射出,这是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
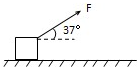 (2011?河南二模)如图所示,质量m=0.78kg的金属块放在水平桌面上,在斜向上的恒定拉力F作用下,向右以v0=2.0m/s的速度作匀速直线运动,已知F=3.0N,方向与水平面之间的夹角θ=37°.(sinθ=0.6,cosθ=0.8,g取10m/s2)
(2011?河南二模)如图所示,质量m=0.78kg的金属块放在水平桌面上,在斜向上的恒定拉力F作用下,向右以v0=2.0m/s的速度作匀速直线运动,已知F=3.0N,方向与水平面之间的夹角θ=37°.(sinθ=0.6,cosθ=0.8,g取10m/s2) 如图所示,质量M=0.2kg的足够长的长板静止在水平地面上,与地面间动摩擦因数μ1=0.1,另一质量m=0.1kg的小滑块以v0=0.9m/s初速滑上长木板,滑块与长木板间动摩擦因数μ2=0.4,求小滑块自滑上长板到最后静止(相对地面)的过程中运动的路程.(可以认为长板与地面间的最大静摩擦力等于滑动摩擦力,g取10m/s2)
如图所示,质量M=0.2kg的足够长的长板静止在水平地面上,与地面间动摩擦因数μ1=0.1,另一质量m=0.1kg的小滑块以v0=0.9m/s初速滑上长木板,滑块与长木板间动摩擦因数μ2=0.4,求小滑块自滑上长板到最后静止(相对地面)的过程中运动的路程.(可以认为长板与地面间的最大静摩擦力等于滑动摩擦力,g取10m/s2)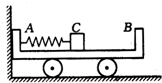 如图所示,质量M=0.8kg的小车静止在光滑的水平面上,左端紧靠竖直墙.在车上左端水平固定着一只弹簧,弹簧右端放一个质量m=0.2kg的滑块,弹簧为原长时,滑块位于C处(滑块可以视为质点),车的上表面AC部分为光滑水平面,CB部分为粗糙水平面.CB长l=1m、与滑块的摩擦因数μ=0.4.水平向左推动滑块,将弹簧压缩,然后再把滑块从静止释放,在压缩弹簧过程中推力做功2.5J,滑块释放后将在车上往复运动,最终停在车上某处.设滑块与车的B端碰撞时机械能无
如图所示,质量M=0.8kg的小车静止在光滑的水平面上,左端紧靠竖直墙.在车上左端水平固定着一只弹簧,弹簧右端放一个质量m=0.2kg的滑块,弹簧为原长时,滑块位于C处(滑块可以视为质点),车的上表面AC部分为光滑水平面,CB部分为粗糙水平面.CB长l=1m、与滑块的摩擦因数μ=0.4.水平向左推动滑块,将弹簧压缩,然后再把滑块从静止释放,在压缩弹簧过程中推力做功2.5J,滑块释放后将在车上往复运动,最终停在车上某处.设滑块与车的B端碰撞时机械能无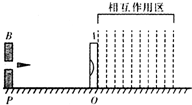 如图所示:质量M=0.40kg的靶盒A位于光滑水平导轨上,开始时静止在O点,在O点右侧有范围很广的“相互作用区域”,如图中划虚线部分所示,当靶盒A进入相互作用区时便受指向O点的恒力F=20N作用,P处有一固定的发射器B,它可根据需要瞄准靶盒并每次发射一颗水平速度υ0=50m/s、质量m=0.10kg的子弹,当子弹打入靶盒A后,便留在盒内,碰撞时间极短.现约定,每当靶盒A停在或到达O点时,都有一颗子弹进入靶盒A内.
如图所示:质量M=0.40kg的靶盒A位于光滑水平导轨上,开始时静止在O点,在O点右侧有范围很广的“相互作用区域”,如图中划虚线部分所示,当靶盒A进入相互作用区时便受指向O点的恒力F=20N作用,P处有一固定的发射器B,它可根据需要瞄准靶盒并每次发射一颗水平速度υ0=50m/s、质量m=0.10kg的子弹,当子弹打入靶盒A后,便留在盒内,碰撞时间极短.现约定,每当靶盒A停在或到达O点时,都有一颗子弹进入靶盒A内.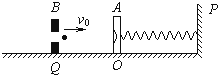 如图所示,质量M=0.040kg的靶盒A静止在光滑水平导轨上的O点,水平轻质弹簧一端栓在固定挡板P上,另一端与靶盒A连接,Q处有一固定的发射器B,它可以瞄准靶盒发射一颗水平速度为v0=50m/s,质量m=0.010kg的弹丸,当弹丸打入靶盒A后,便留在盒内,碰撞时间极短,不计空气阻力,求
如图所示,质量M=0.040kg的靶盒A静止在光滑水平导轨上的O点,水平轻质弹簧一端栓在固定挡板P上,另一端与靶盒A连接,Q处有一固定的发射器B,它可以瞄准靶盒发射一颗水平速度为v0=50m/s,质量m=0.010kg的弹丸,当弹丸打入靶盒A后,便留在盒内,碰撞时间极短,不计空气阻力,求