题目内容
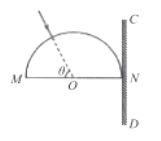
【题目】如图,玻璃柱的横截面为半径R=20.0 cm的半圆,O点为圆心。光屏CD紧靠在玻璃柱的右侧,且与截面底边MN垂直。一光束沿中半径方向射向O点,光束和MN的夹角为![]() ,在光屏CD上出现两个光斑。己知玻璃的折射率为n=
,在光屏CD上出现两个光斑。己知玻璃的折射率为n=![]() 。
。
(i)若![]() =60°,求两个光斑间的距离;
=60°,求两个光斑间的距离;
(ii)屏上两个光斑间的距离会随![]() 大小的变化而改变,求两光斑间的最短距离。
大小的变化而改变,求两光斑间的最短距离。
【答案】(i)![]() cm;(ii)20
cm;(ii)20![]() cm
cm
【解析】
(i)光束在MN界面上一部分反射,设反射光与光屏CD的交点为C,另一部分折射,设折射光与光屏的交点为D,入射角为r,折射角为i,光路图如图所示,由几何关系得:r=90°-θ=30°
得:![]()
根据折射定律得 ![]()
可得,i=60°
则![]()
所以两个光斑间的距离 LCD=LCN+LDN=![]()

(ii)屏上两个光斑间的距离会随θ的减小而变短,当光线在MN就要发生全反射时,两光斑间距离最短,由临界角公式![]() 得:
得:![]()
所以两光斑间的最短距离 Lmin=![]()
联立解得 Lmin=20![]() cm
cm

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案【题目】图甲为欧姆表的电路原理图,可将欧姆表内部(图中虚线框内)等效为一电源。设计图乙电路测量欧姆表某挡位的电动势与内阻,具体操作如下:
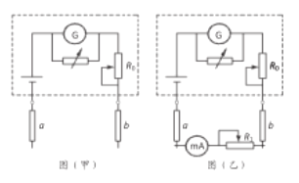
A.将欧姆表的_______旋至某挡位,a、b两表笔短接,调节调零旋钮进行_____;
B.将毫安表与滑动变阻器R1按图乙连接;
C.调节消动变阻器R1滑片的位置,读出亳安表的示数
I和对应的欧姆表示数R,将多组数据填入表中。
1 | 2 | 3 | 4 | 5 | 6 | |
R/kΩ | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
I/mA | 1.48 | 1.20 | 1.03 | 0.86 | 0.74 | 0.67 |
1/I/mA-1 | 0.68 | 0.83 | 0.97 | 1.16 | 1.35 | 1.49 |
完成下列内容:
(1)填写操作A中横线上的内容:
(2)图甲中a为__________(选填“红”、“黑”)表笔;
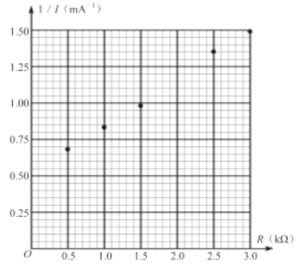
(3)根据表中数据描点(第四组数据) 并画出![]() 关系图象__________;
关系图象__________;
(4)由图象可得欧姆表该档位的电动势为__________V,内阻为__________kΩ。(结果均保留两位有效数字)