��Ŀ����
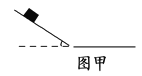
����Ŀ����ͼ��ʾ�������ֲ����ȡ��뾶ΪR�Ĺ⻬��Բ�ν����ۣ���ֹ�ڹ⻬��ˮƽ���ϣ���߽�����ֱǽ�ڣ�һ����Ϊm��С��Ӿ�������϶�R���ɾ�ֹ���䣬ǡ���������������н�����ڣ�������͵�������˶��ӽ����۵��Ҷ˳����С����ߵ�ʱ�������Բ����͵�ľ���Ϊ ![]() R���������ٶ�Ϊg�����ƿ�����������
R���������ٶ�Ϊg�����ƿ�����������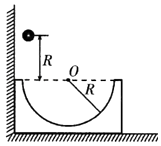
��1��С���һ�ε�����͵�ʱ�Խ����۵�ѹ����С��
��2�������۵�������
���𰸡�
��1���⣺С��Ӿ�ֹ����һ�ε�����͵�Ĺ��̣����ݻ�е���غ㶨���У�
mg2R= ![]()
С��յ���͵�ʱ������Բ���˶���ţ�ٵڶ����ɵ�֪ʶ�У�
FN��mg=m ![]()
��ţ�ٵ������ɿ�֪С��Խ������ѹ��Ϊ��FN��=FN
������ã�FN��=5mg
��С���һ�ε�����͵�ʱ��С��Խ������ѹ��Ϊ5mg��
��2���⣺С���һ�ε�����͵���С����ߵ���̣�С��ͽ�����ˮƽ�������غ㣬ѡȡ����Ϊ��������
mv0=��m+M��v
��С����ߵ�ʱ�������Բ����͵�ĸ߶�Ϊh��
���� R2+h2= ![]()
���������غ㶨���У�mgh= ![]() ��
�� ![]() ��m+M��v2��
��m+M��v2��
������ã�M= ![]() m
m
�𣺽����������Ϊ ![]() m��
m��
����������1���ɻ�е���غ����С���һ�ε�����͵���ٶȣ���ţ���˶��������С������͵�Խ������ѹ������2��С���һ�ε�����͵���������ߵ�Ĺ����У��������뿪ǽ�ڣ�С��ͽ�������ɵ�ϵͳˮƽ�������غ㣬ϵͳ�Ļ�е��Ҳ�غ㣬�ɶ����غ㶨�ɺͻ�е���غ㼴����������۵�������
�����㾫����������Ҫ�������������Ͷ����غ㶨�ɵ����֪ʶ�㣬��Ҫ��������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ���������������غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��������ȷ�����⣮

 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�