��Ŀ����
����Ŀ����12�֣���ͼ���ף���ʾ��ABCO�ǹ̶���һ���T��֧�ܣ�ˮƽ����AC������ΪM=2 kg������ΪL=1 m�����ʱ��壬OB������Ӳ�ˣ��¶�ͨ���⻬����������ˮƽ�����ϣ�֧�ܿ���ˮƽ��O����ֱ��������ת����A�˸�������ƽ̨������֪AB����l1=0.75 m��OB����h=0.5 m������һ����Ϊm=2 kg����飨����Ϊ�ʵ㣩��v0=3 m/s��ˮƽ���ٶȻ���AC�壬�����AC�䶯Ħ��������=0.5���ʣ�T��֧���Ƿ����O�ᷭת��ijͬѧ�Ľ���˼·���£�
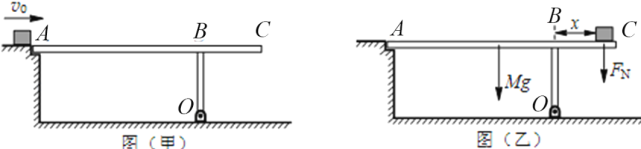
֧�����������ͼ���ң�����֧�ܼ�����תʱ���λ��B���Ҳ�x������������ƽ�ⷽ�̣�Mg(l1�C![]() )=FN��x��ʽ��FN=mg�����x=0.2 m��
)=FN��x��ʽ��FN=mg�����x=0.2 m��
��ʱ�����A��s1=l1+x=0.95 m��
Ȼ����������v0=3 m/s�ij��ٶ���AC������ܻ��еľ���s2���Ƚ����������룺��s2��s1����T��֧�ܲ�����O�ᷭת����s2>s1�������O�ᷭת��
���жϸ�ͬѧ�Ľ���˼·�Ƿ���ȷ������ȷ���밴�ո�˼·����������̲���������������������������ȷ����ָ����ͬѧ�Ĵ���֮����������ȷ�ķ�����������
���𰸡���ͬѧ��˼·����ȷ����ͬѧ����֧������ʱ��©��������AC��Ħ����������ƽ�ⷽ���д���T��֧�ܻ���O�ᷭת��
����������ͬѧ��˼·����ȷ����2�֣�
��ͬѧ����֧������ʱ��©��������AC��Ħ����������ƽ�ⷽ���д�����������AC��Ħ����������ƽ�ⷽ��Ϊ��![]() ��2�֣�
��2�֣�
ʽ��FN=mg��Ff=��FN=��mg��1�֣�
�õ���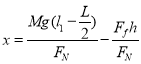 ��2�֣�
��2�֣�
�������ݵ�x=0���������AC����s1=0.75 m����B��ʱ��֧��ǡ�÷�ת
�����AC�ϻ���ʱ������ţ�ٵڶ����ɣ��ã���mg=ma��1�֣�
��ã�a=��g=5 m/s2��1�֣�
�����AC������ܻ��еľ���Ϊ��![]() ��2�֣�
��2�֣�
����s2>s1������T��֧�ܻᷭת��1�֣�

 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�