题目内容
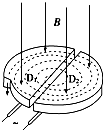
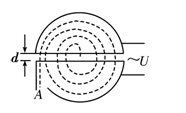
图是回旋加速器的原理图,设在D型盒上半面中心出口处A有一正离子源(离子出发时初速不计),正离子的带电量为q,质量为m,加速时电极间电压大小为U,磁场的磁感强度为B,求:
(1)离子在下半盒中第1条和第k条轨道半径之比为为多少?
(2)设D型盒的半径为R,离子能获得的最大动能为多少?

(1)离子在下半盒中第1条和第k条轨道半径之比为为多少?
(2)设D型盒的半径为R,离子能获得的最大动能为多少?

(1)根据动能定理可知,设离子在下半盒中第1条的速度v1;则有:qU=
m
;
当在第k条轨道速度,则有:(2k-1)qU=
m
;
又由洛伦兹力提供向心力,结合牛顿第二定律,则有:R1=
,
而第k条轨道半径,Rk=
;
因此第1条和第k条轨道半径之比为R1:Rk=
:
=1:
;
(2)当粒子的半径达最大时,必须将带电粒子引出,此时由Bqv=m
可得:
v=
,则最大动能Ek=
mv2=
;
答:(1)离子在下半盒中第1条和第k条轨道半径之比为1:
;
(2)设D型盒的半径为R,离子能获得的最大动能为=
.
| 1 |
| 2 |
| v | 21 |
当在第k条轨道速度,则有:(2k-1)qU=
| 1 |
| 2 |
| v | 2k |
又由洛伦兹力提供向心力,结合牛顿第二定律,则有:R1=
| mv1 |
| Bq |
而第k条轨道半径,Rk=
| mvk |
| Bq |
因此第1条和第k条轨道半径之比为R1:Rk=
|
|
| 2k-1 |
(2)当粒子的半径达最大时,必须将带电粒子引出,此时由Bqv=m
| v2 |
| R |
可得:
v=
| BqR |
| m |
| 1 |
| 2 |
| B2q2R2 |
| 2m |
答:(1)离子在下半盒中第1条和第k条轨道半径之比为1:
| 2k-1 |
(2)设D型盒的半径为R,离子能获得的最大动能为=
| B2q2R2 |
| 2m |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目