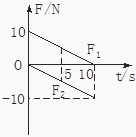��Ŀ����
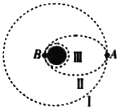
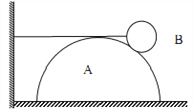
����Ŀ����ͼ��ʾ������ΪM���뾶Ϊ4R�İ�����Aʼ�վ�ֹ�ڴֲ�ˮƽ���ϣ�����Ϊm���뾶ΪR�Ĺ⻬С��Bͨ��һ���������A��ߵ����е����Ӵ���ˮƽϸ��ϵס��ֹ�ڰ�����A�ϡ���֪�������ٶ�Ϊg������˵����ȷ���ǣ� ��
A. ϸ�߶�С���������СΪ![]()
B. ����������Ħ�����Ĵ�СΪ![]()
C. ����С���λ�ú;�ֹ״̬���䣬��ϸ���������ֱǽ�������ƣ�ϸ�߶�С�������
������
D. ����B�����ӵ�˲�䣬С��B�ļ��ٶȴ�СΪ0.6g
���𰸡�AD
��������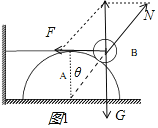
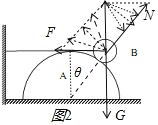
A. ��С���������������ͼ1��֪��С����������֧���������ӵ��������ö�����ƽ��״̬���ɼ��ι�ϵ��֪��sin��=4R/5R=0.8������=53�����ɼ��ι�ϵ֪��F=mgtan��= ![]() ����A��ȷ��
����A��ȷ��
B. �ɼ��ι�ϵ��ã�N=mg/cos��=5mg/4����ţ�ٵ������ɿ�֪��С��������ѹ��Ϊ��N��=5mg/4�������������ˮƽ������Ħ������N���ķ���ƽ�������У�f=N��sin��=3mg/4����B������
C. ����С���λ�ú;�ֹ״̬���䣬��ϸ���������ֱǽ�������ƣ���ϸ������ֱ����ļн�Խ��ԽС������ͼ2��֪��ϸ�߶�С��������ȼ�С������C����
D. ����B�����ӵ�˲�䣬С����������ͻ�䣬��ʱ����F��=mgcos��=0.6mg����ţ�ٵڶ����ɿɵã����ٶ�Ϊ0.6g����D��ȷ��
��ѡ��AD.

 �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д� ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�