题目内容
如图所示,木块 A 与 B 用一轻弹簧相连,竖直放在木块 C 上,三者静置于地面上,它们的质量之比是1:2:3.设所有接触面都光滑,在沿水平方向抽出木块 C 的瞬间,木块 A 和 B 的加速度分别是( )
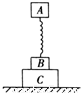
A.aA=0
B.aA=g
C.aB=3g
D.aB=
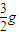
【答案】分析:抽出木块C之前,对木块A和木块B分别受力分析,运用平衡条件求出各个力;抽出木块C后,再次对木块A和木块B受力分析,然后根据牛顿第二定律列式求解.
解答:解:抽出木块C之前,木块A受到重力和支持力,有F=mg ①
木块B受到重力2mg、弹簧向下的弹力F和木块C的支持力N,根据平衡条件,有:N=F+mg ②
解得
N=3mg
撤去木块C瞬间,木块C对B的支持力变为零,木块A受力情况不变,故木块A的加速度为零,木块B受重力2mg和弹簧的压力N=mg,故合力为3mg,故物体B的瞬时加速度为1.5g;
故选A、D.
点评:本题是力学中的瞬时问题,关键是对物体A、B分别受力分析,撤去C物体瞬间再次对物体受力分析,最后运用牛顿第二定律列式求解加速度.
解答:解:抽出木块C之前,木块A受到重力和支持力,有F=mg ①
木块B受到重力2mg、弹簧向下的弹力F和木块C的支持力N,根据平衡条件,有:N=F+mg ②
解得
N=3mg
撤去木块C瞬间,木块C对B的支持力变为零,木块A受力情况不变,故木块A的加速度为零,木块B受重力2mg和弹簧的压力N=mg,故合力为3mg,故物体B的瞬时加速度为1.5g;
故选A、D.
点评:本题是力学中的瞬时问题,关键是对物体A、B分别受力分析,撤去C物体瞬间再次对物体受力分析,最后运用牛顿第二定律列式求解加速度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,木块A放在木块B上左端,用力F将A拉至B的右端,第一次将B固定在地面上,F做功为W1,产生的热量为Q1;第二次让B可以在光滑地面上自由滑动,这次F做的功为W2,产生的热量为Q2,则应有( )
如图所示,木块A放在木块B上左端,用力F将A拉至B的右端,第一次将B固定在地面上,F做功为W1,产生的热量为Q1;第二次让B可以在光滑地面上自由滑动,这次F做的功为W2,产生的热量为Q2,则应有( )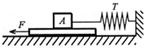 如图所示,木块A放在粗糙的长木板B上,B放在粗糙水平地面上,在水平恒力F作用下,B以速度v向左匀速运动,该过程中水平弹簧秤的示数稳定为T.下列说法中正确的是( )
如图所示,木块A放在粗糙的长木板B上,B放在粗糙水平地面上,在水平恒力F作用下,B以速度v向左匀速运动,该过程中水平弹簧秤的示数稳定为T.下列说法中正确的是( )| A、木块受到的静摩擦力大小等于T | B、木板B向左匀速运动的速度越大所需的拉力F越大 | C、若用2F的力作用在木板上,木块受到的摩擦力的大小等于T | D、若木板以2a的加速度运动时,木块受到的摩擦力大小等于T |
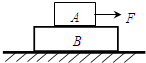 如图所示,木块A的质量为m,木块B的质量为M,叠放在光滑的水平面上,A、B之间的滑动摩擦因数为μ,若最大静摩擦力等于滑动摩擦力,重力加速度为g.现用水平力F作用于A,则保持A、B相对静止的条件是F不超过( )
如图所示,木块A的质量为m,木块B的质量为M,叠放在光滑的水平面上,A、B之间的滑动摩擦因数为μ,若最大静摩擦力等于滑动摩擦力,重力加速度为g.现用水平力F作用于A,则保持A、B相对静止的条件是F不超过( ) 如图所示,木块A、B分别重50N和70N,它们与水平地面之间的动摩擦因数均为0.2,与A、B相连接的轻弹簧被压缩了5cm,系统置于水平地面上静止不动.已知弹簧的劲度系数为100N/m.现用F=7N的水平力作用在木块A上后,木块A所受摩擦力大小为
如图所示,木块A、B分别重50N和70N,它们与水平地面之间的动摩擦因数均为0.2,与A、B相连接的轻弹簧被压缩了5cm,系统置于水平地面上静止不动.已知弹簧的劲度系数为100N/m.现用F=7N的水平力作用在木块A上后,木块A所受摩擦力大小为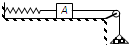 如图所示,木块A放在水平桌面上.木块左端用轻绳与轻质弹簧相连,弹簧的左端固定,用一轻绳跨过光滑定滑轮,一端连接木块右端,另一端连接一砝码盘(装有砝码),轻绳和弹簧都与水平桌面平行.当砝码和砝码盘的总质量为0.5kg时,整个装置静止,弹簧处于伸长状态,弹力大小为3N.若轻轻取走盘中的部分砝码,使砝码和砝码盘的总质量减小到0.1kg,取g=10m/s2,此时装置将会出现的情况是( )
如图所示,木块A放在水平桌面上.木块左端用轻绳与轻质弹簧相连,弹簧的左端固定,用一轻绳跨过光滑定滑轮,一端连接木块右端,另一端连接一砝码盘(装有砝码),轻绳和弹簧都与水平桌面平行.当砝码和砝码盘的总质量为0.5kg时,整个装置静止,弹簧处于伸长状态,弹力大小为3N.若轻轻取走盘中的部分砝码,使砝码和砝码盘的总质量减小到0.1kg,取g=10m/s2,此时装置将会出现的情况是( )