题目内容
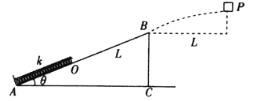
【题目】如图所示,倾角为θ=37°的斜面体固定在水平地面上,一根劲度系数为k的轻弹簧放在斜面上,与斜面底端的固定挡板相连,轻弹簧的上端与斜面上的O点对齐,斜面OA段光滑,OB段粗糙,一个质量为m的物块从P点水平抛出,刚好从斜面顶端B点滑上斜面且速度方向与斜面平行,P点与B点的水平距离为L,重力加速度为g,物块与斜面OB段的动摩擦因数为0.5,OB长等于L,不计物块的大小,sin37°=0.6,cos37°=0.8,求:
(1)物块第一次运动到O点的速度大小;
(2)试分析物块能否滑离斜面,如果能滑离,滑离后物块在空中的最小速度多大;如果不能滑离,物块在斜面OB段运动的距离是多少。
【答案】(1)![]() ; (2)能,
; (2)能,![]()
【解析】
(1)物块从P点抛出后做平抛运动,到B点时速度的反向延长线交于水平位移的中点,设P点和B点的高度差为h,则
![]()
设物块从P点抛出的速度为v0,则
![]()
![]()
解得
![]()
设物块第一次运动到O点时的速度为v1,根据动能定理有
![]()
解得
![]()
(2)设物块不能滑离斜面,设物块从O点向上滑到斜面最高点时离O点距离为x,根据动能定理有
![]()
解得
![]() ,
,
因此假设不成立,物块会滑离斜面
设滑离斜面时物块的速度大小为v2,根据动能定理有
![]()
解得
![]()
物块在B点抛出后,做斜上抛运动,运动到最高点时速度最小,最小速度为
![]()

练习册系列答案
相关题目