题目内容
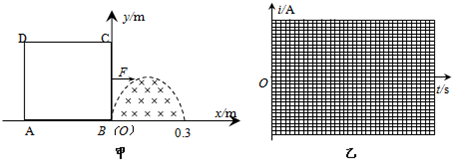
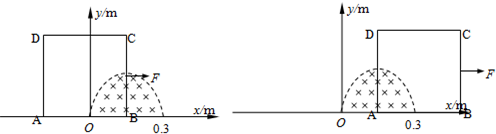
如图甲所示,光滑绝缘水平桌面上直立一个单匝正方形导线框ABCD,线框的边长为L=0.4m、总电阻为R=0.1Ω.在直角坐标系xoy中,有界匀强磁场区域的下边界与x轴重合,上边界满足曲线方程y=0.2sin
x(m),场强大小B=0.2T.线框在沿x轴正方向的拉力F作用下,以速度v=10m/s水平向右做匀速直线运动,恰好拉出磁场.
(1)求线框中AD两端的最大电压;
(2)在图乙中画出运动过程中线框i-t图象,并估算磁场区域的面积;
(3)求线框在穿越整个磁场的过程中,拉力F所做的功.
| 10π | 3 |

(1)求线框中AD两端的最大电压;
(2)在图乙中画出运动过程中线框i-t图象,并估算磁场区域的面积;
(3)求线框在穿越整个磁场的过程中,拉力F所做的功.
分析:(1)线框中BC或AD切割磁感线时,产生的感应电动势为E=Byv,则知当AD边运动到磁场中心时,AD边上的电压最大.由E=BLv、I=
、U=IR结合求解AD两端的最大电压;
(2)由t=
求出BC边切割磁场的时间,确定出没有电流的时间,画出i-t图象.i-t图象与坐标轴所围“面积”大小等于电量,估算出电量Q,根据电量Q=
=
求出磁场区域的面积.
(3)在t1和t3时间内,通过线框的电流按正弦规律变化,求出电流的有效值.拉力做功等于线框中产生的电能,根据焦耳定律和功能关系求解拉力F所做的功.
| E |
| R |
(2)由t=
| x |
| v |
| △Φ |
| R |
| BS |
| R |
(3)在t1和t3时间内,通过线框的电流按正弦规律变化,求出电流的有效值.拉力做功等于线框中产生的电能,根据焦耳定律和功能关系求解拉力F所做的功.
解答:解:(1)当导线框运动到磁场中心线时,有两种情况,一是BC边,二是AD边,当AD边运动到磁场中心时,AD边上的电压最大.
Em=Bymv=0.2×0.2×10V=0.4V
Im=
=
A=4A
则线框中AD两端的最大电压是Um=Im?
R=4×
×0.1V=0.3V
(2)BC边切割磁场的时间为t1=
s=0.03s
此后,经t2时间,线框中无感应电流
t2=
s=0.01s
AD边切割时间t3=t1=0.03s
在整个切割过程中,i-t图象如图所示.
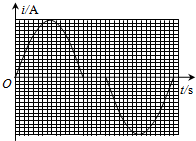
由图象可知,每个小方格表示电量q=0.0005C
在图象中,图象与t轴所围区域共有小方格153个,故t1时间内通过线框某一截面的电量 Q=Nq=153×0.0005C=0.0765C
又Q=
=
得S=
=0.038m2
(3)在t1和t3时间内,通过线框的电流按正弦规律变化
电流的有效值为 I=
Im=
×4A=2
A
由于线框做匀速运动,则根据功能关系得
W=I2R(t1+t3)=0.048J
答:(1)求线框中AD两端的最大电压是0.3V;
(2)在图乙中画出运动过程中线框i-t图象如图所示,磁场区域的面积是0.038m2;
(3)线框在穿越整个磁场的过程中,拉力F所做的功是0.048J.

Em=Bymv=0.2×0.2×10V=0.4V
Im=
| Em |
| R |
| 0.4 |
| 0.1 |
则线框中AD两端的最大电压是Um=Im?
| 3 |
| 4 |
| 3 |
| 4 |
(2)BC边切割磁场的时间为t1=
| 0.3 |
| 10 |
此后,经t2时间,线框中无感应电流
t2=
| 0.4-0.3 |
| 10 |
AD边切割时间t3=t1=0.03s
在整个切割过程中,i-t图象如图所示.

由图象可知,每个小方格表示电量q=0.0005C
在图象中,图象与t轴所围区域共有小方格153个,故t1时间内通过线框某一截面的电量 Q=Nq=153×0.0005C=0.0765C
又Q=
| △Φ |
| R |
| BS |
| R |
得S=
| QR |
| B |
(3)在t1和t3时间内,通过线框的电流按正弦规律变化
电流的有效值为 I=
| ||
| 2 |
| ||
| 2 |
| 2 |
由于线框做匀速运动,则根据功能关系得
W=I2R(t1+t3)=0.048J
答:(1)求线框中AD两端的最大电压是0.3V;
(2)在图乙中画出运动过程中线框i-t图象如图所示,磁场区域的面积是0.038m2;
(3)线框在穿越整个磁场的过程中,拉力F所做的功是0.048J.
点评:本题是产生正弦式交变电流的一种方式,是法拉第电磁感应定律、欧姆定律、焦耳定律等等知识的综合应用,难点是运用近似方法估算出i-t图象的面积,求出电量,再根据经验公式Q=
,求出面积S.
| △Φ |
| R |

练习册系列答案
相关题目
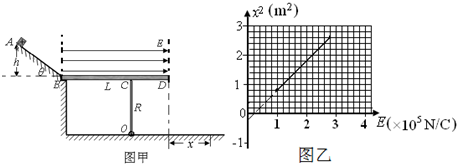
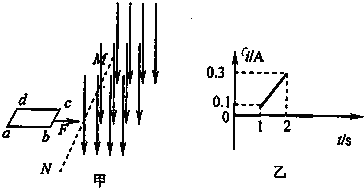
 中,线圈中感应电流I随时间t变化的图象如图乙所示.求:
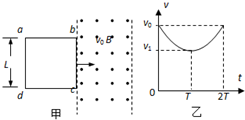
中,线圈中感应电流I随时间t变化的图象如图乙所示.求: (2011?崇明县二模)如图甲所示,光滑绝缘的水平面上一矩形金属线圈 abcd的质量为m、电阻为R、面积为S,ad边长度为L,其右侧是有左右边界的匀强磁场,磁场方向垂直纸面向外,磁感应强度大小为B,ab边长度与有界磁场区域宽度相等,在t=0时刻线圈以初速度v0进入磁场,在t=T时刻线圈刚好全部进入磁场且速度为vl,此时对线圈施加一沿运动方向的变力F,使线圈在t=2T时刻线圈全部离开该磁场区,若上述过程中线圈的v-t图象如图乙所示,整个图象关于t=T轴对称.则下列各项正确的是( )
(2011?崇明县二模)如图甲所示,光滑绝缘的水平面上一矩形金属线圈 abcd的质量为m、电阻为R、面积为S,ad边长度为L,其右侧是有左右边界的匀强磁场,磁场方向垂直纸面向外,磁感应强度大小为B,ab边长度与有界磁场区域宽度相等,在t=0时刻线圈以初速度v0进入磁场,在t=T时刻线圈刚好全部进入磁场且速度为vl,此时对线圈施加一沿运动方向的变力F,使线圈在t=2T时刻线圈全部离开该磁场区,若上述过程中线圈的v-t图象如图乙所示,整个图象关于t=T轴对称.则下列各项正确的是( )