Question

【题目】如图所示，质量m=lkg的物块从h=0.8m高处沿光滑斜面滑下，到达底部时通过光滑圆弧BC滑至水平传送带CD上，CD部分长L=2m．传送带在皮带轮带动下．以v=4m/s的速度逆时针传动，物块与传送带间动摩擦因数μ=0.3，求：

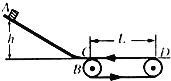
（1）物块滑到C、D两点时的速度大小各为多少？

（2）物块从C滑到D的过程中，皮带对物块做多少功？

（3）物块从C滑到D的过程中，因摩擦产生的热量是多少？

Answer 1

【答案】(1) 4m/s 2m/s (2) ﹣6J (3) 14J

【解析】试题分析：根据机械能守恒定律求出物块滑动C点的速度，根据牛顿第二定律求出物块在传送带上的加速度，通过运动学公式求出物块到达D点的速度大小；根据动能定理求出物块从C滑到D的过程中，皮带对物块做功的大小；根据运动学公式求出物块与传送带发生的相对位移，通过Q=f△s求出产生的热量。

（1）由机械能守恒定律得

解得物块到达C点的速度：vC=4m/s．

物块在皮带上滑动的加速度a=μg=3m/s2由运动学公式得，

解得物块到达D点的速度vD =2m/s．

（2）皮带对物块做功W=﹣μmgL=﹣6J．

（3）物块从C点滑动D的时间

物块与皮带相对滑动的距离s1=vt1+L

物块在皮带上滑动的过程中产生的热量Q=μmgs1=14J。