Question

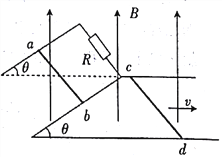
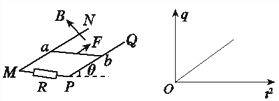
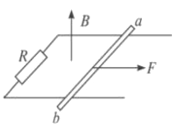
【题目】如图所示，水平放置的金属导轨上连有电阻R，并处在垂直于轨道平面的匀强磁场中.今从静止起用力拉金属棒ab(与轨道垂直)，用以下两种方式拉金属棒.若拉力恒定，经时间后ab的速度为v，加速度为，最终速度可达2v；若拉力的功率恒定，经时间后，ab的速度也是v，加速度为，最终速度可达2v.求和满足的关系。

Answer 1

【答案】

【解析】试题分析：推导出棒的速度为v和2v时所受的安培力大小．由于两种情况下棒最终都做速度为2v的匀速运动，拉力与安培力平衡，根据牛顿第二定律和功率公式P=Fv求出两个加速度的关系。

棒的速度为v时，产生的电动势为：

感应电流为：

所受的安培力为：

联立可得：

同理：棒的速度为2v时，所受的安培力为：

两种情况下，棒最终做匀速运动的速度均为2v，此时的拉力均为：

若F恒定，ab棒速度为v时，根据牛顿第二定律：

联立以上解得：

若P恒定，则得拉力的功率为：

ab棒速度为v时，拉力为：

此时ab棒的加速度为：

联立解得：

所以：a2=3a1