题目内容
【题目】如图所示,质量分别为m1、m2的木块用轻弹簧相连,静止在光滑的水平地面上,m2与墙壁挨在一起,质量为m的子弹用速度为v0的水平初速度射入木块m1中,并留在m1中,求子弹射入m1以后的过程中,轻弹簧压缩到最短时的弹性势能 . 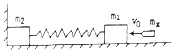
【答案】![]()
【解析】解:设子弹打入木块m1后瞬间的速度为v,在子弹射入木块m1的过程中,取向左为正方向,根据动量守恒定律得:
mv0=(m+m1)v…①
m1和子弹一起运动向左压缩弹簧,它们的动能转化为弹簧的弹性势能,根据能量守恒定律得:
轻弹簧压缩到最短时的弹性势能为:Ep= ![]() (m+m1)v2.
(m+m1)v2.
联立解得:Ep= ![]()
所以答案是: ![]() .
.
【考点精析】利用动量守恒定律对题目进行判断即可得到答案,需要熟知动量守恒定律成立的条件:系统不受外力或系统所受外力的合力为零;系统所受的外力的合力虽不为零,但系统外力比内力小得多;系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变.

练习册系列答案
相关题目