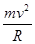Question

竖直平面内光滑圆轨道外侧，一小球以某一水平速度v₀从A点出发沿圆轨道运动，至B点时脱离轨道，最终落在水平面上的C点，不计空气阻力．下列说法中不正确的是

A．在B点时，小球对圆轨道的压力为零

B．B到C过程，小球做匀变速运动

C．在A点时，小球对圆轨道压力大于其重力

D．A到B过程，小球水平方向的加速度先增加后减小

Answer 1

C

小球从A点到B点 重力做正功，A到B过程中小球动能增加。小球在B点时候对圆滑轨道的压力为0 ，只受重力。 F向=mrω² =mv²/r ，速度增大，向心力增大，故向心加速度增大。小球在A到B的过程中。假设AB两点夹角为A 。十字分解法，mgcos A-N=mv²/r ，Nsin A=水平方向分力 我们知道小球的速度是不断增大的，那么支持力N就越来越小。在A点的时候，水平方向没有力。在B点的时候，小球脱离了轨道，只受重力。故也没有水平力。所以说是先增大后减小。这个最大点不好计算出来，跟小球在A点的初速度大小有关。C错，ABD正确。故本题选C。