��Ŀ����
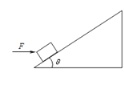
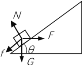
����Ŀ������Ϊ10kg��������![]() N��ˮƽ���������£����ϱ���ֲڡ��̶�б��ĵ�A�ɾ�ֹ��ʼ��б�������˶�����֪б�泤
N��ˮƽ���������£����ϱ���ֲڡ��̶�б��ĵ�A�ɾ�ֹ��ʼ��б�������˶�����֪б�泤![]() �ף����
�ף����![]() ��������б���Ķ�Ħ������
��������б���Ķ�Ħ������![]() �������������ƣ�
�������������ƣ�
��1�������������������������ʾ��ͼ�����������ܵ�����Ħ������С��
��2�������������˶��ļ��ٶȴ�С��
��3������������3m��ȥ����F�������ܷ�б����ߵ�B��˵������,��������嵽�����ʱ�Ķ��ܴ�С��
���𰸡���1��
 ��Ħ����
��Ħ����![]() ��
��
��2��a1=6m/s2
��3��328J
��������
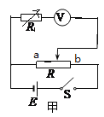
��1����������ͼ��
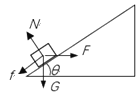
��ֱб�淽��ƽ�⣺FN =mgcos��+Fsin��
Ff=��FN=��(mgcos��+Fsin��)
�������ݽ����Ff=40N
��2�� ��б�淽��ţ�ٶ��ɣ�Fcos����Ff��mgsin��=ma
�����a1=(Fcos����Ff��mgsin��)/m
�������ݽ����a1=6m/s2
��3�� ��ȥF����ţ�ٵڶ����ɣ�mgsin��+��mgcos��=ma2
a2=7.6m/s2
��ȥF˲�䣬�����ٶ���Ϊv1
��v12=2aS1�����v1=![]() =6m/s
=6m/s
���˶���ֹͣ��Ҫ�ľ���ΪS2
�� v12=2a2S2 S2=2.37m
S2>S=2m���������ܹ�������ߵ�B
����B��ʱ�ٶ�Ϊv2������v12- v22=2a2S
v22=5.6������Ek2=![]() =28J
=28J
B��߶�h=ABsin37��=3m
B����������Ep2=mgh=300J
�뿪B��������׳�б����أ���е���غ�,�����Ϊ�����ܵ�
Ek2+ Ep2= Ek3
Ek3=328J