题目内容
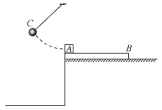
【题目】如图所示，质量M=lkg的长木板B置于粗糙的平台上，在长木板的左侧有一质量
=3kg的物块A，物块A与木板B之间的动摩擦因数为
=0.2.质量为
=lkg的小球C用轻质细线悬挂于物块A的正上方，将小球C向左拉至某一个高度，由静止释放，释放时小球C和物块A之间的高度差为h=3.2 m.小球C和物块A发生弹性正碰的瞬间细线断裂.与此同时，对长木板B施加一大小F=14N，方向水平向右的恒力.当A与B速度相同时，物块A距长木板B的左端为
m，取重力加速度g=10m/s.试求：
(1)小球C和物块A发生弹性正碰后，物块A的速度为多少?
(2）长木板B与地面间的动摩擦因数
；
(3）在A、B速度达到相同后，再经过t时间，撤去水平恒力F，求t满足什么条件时，无论长木板多长，物块都会滑出长木板.(结果可保留根号)
【答案】（1）
（2）
（3）故当
时，无论长术板多长，物块都会滑出长木板.
【解析】(1)根据机械能守恒定律：
解得：v0=8m/s
据动量守恒定律和机械能守恒：m1v0=m1v1+m2v2
解得：v1=-4m/s，v2=4m/s
设A、B共同的速度为
，根据平均速度公式可知：
，
xA-xB=4m/9
解得：
，
故长木板B的加速度
对长木板B受力分析。根据牛顿第二定律可知：
解得：
（3)在A、B速度相同后，A的加速度：
B的加速度清足
解得：
在t时间内，长木板B的位移为：
物块A的)位移为：
撒去F后，物块A继续加速，木板B减速，两者共速后，由于μ1>μ2，所以A、B以相同的加速度一起减速。
故使物块A一定能滑出长木板B的临界条件是两者共速时，A刚好到B的左边缘上，
设撤去力下到共速.时间为t′
此时木板加速度满足：
解得：
t′时间内，物块人的位移为：
B的位移为：
由于两者最终共速故有：
由于最终A在B的左边缘上，所以
解得：t=
s，故当时，无论长木板多长，物块都会滑出长木板.
