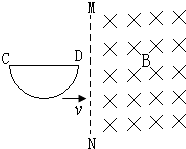
题目内容
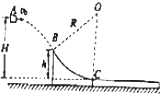
【题目】某实验小组用图甲所示装置研究系统在金属轨道上运动过程中机械能是否守恒：将一端带有滑轮的长金属轨道水平放置，重物通过细绳水平牵引小车沿轨道运动，利用打点计时器和纸带记录小车的运动．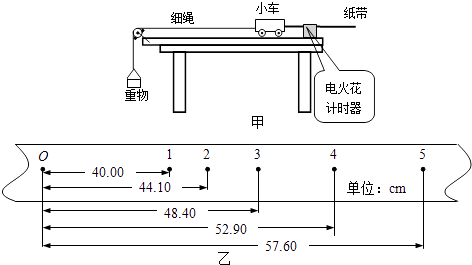
（1）本实验中小车质量（填“需要”、“不需要”）远大于重物质量；
（2）将小车靠近打点计时器，将穿好的纸带拉直，接通电源，释放小车．图乙是打出的一条清晰纸带，O点是打下的第一个点，1、2、3、4、5是连续的计数点，O点和计数点1之间还有多个点（图中未画出），相邻计数点间的时间间隔为0.02s．在打计数点4时小车的速度v=m/s（保留三位有效数字）．若已知重物的质量为m，小车的质量为M，则从点O到点4的过程中，系统减少的重力势能为J，增加的动能为J（g取9.8m/s2 ， 数字保留两位小数）．
【答案】
（1）不需要
（2）2.30,5.18m,2.65（m+M）
【解析】解：（1）本实验中为了验证机械能守恒定律，两物体的质量均要考虑，故不需要使小车的质量远小于重物的质量；（2）打4点时的速度v= 
= 
=2.30m/s；
0到4过程中重力势能的减小量△EP=mgh=9.8×0.5290m=5.18m；
动能的增加量△Ek= 
（m+M）v2= ×（2.3）2（M+m）=2.65（M+m）
故答案为：（1）不需要；（2）2.30；5.18m； 2.65（m+M）．
（1）明确实验原理，根据机械能守恒定律进行分析即可明确是否需要小车的质量远小于重物的质量；（2）根据平均速度方法可求得打点4时的速度；根据重力势能的定义可求得0到4时的改变量；根据动能的定义可求得动能的变化．
练习册系列答案
相关题目
