��Ŀ����
����Ŀ����ͼ��ʾ��һ������Բ����ij����ˮƽ�̶���Բ�����ֱ���˷ֱ��������ֱ������У��뾶R=0.5m�����A��V0=6m/s���ٶȻ���Բ�����������ߵ�Q������Բ�����������ֱ����P����ֹ�����B��ײ������ճ��һ���˶���P��������⻬���Ҳ����ʴֲڶΣ��⻬�ν������У�ÿ�γ��ȶ�ΪL=0.1m���������ֲڶμ�Ķ�Ħ��������Ϊ��=0.1��A��B��������Ϊm=1kg���������ٶ�gȡ10m/s2��A��B��Ϊ�ʵ㣬��ײʱ�伫�̣���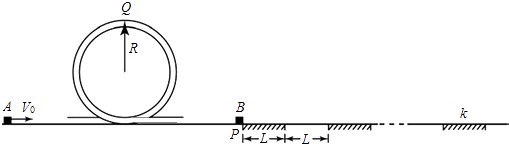
��1����A����Q��ʱ���ٶȴ�СV���ܵ��ĵ�����СF��
��2��������AB����ֹͣ�ڵ�k���ֲڶ��ϣ���k����ֵ��
��3��������AB������n����n��k���⻬���ϵ��ٶ�VAB��n�Ĺ�ϵʽ��
���𰸡�
��1��
�⣺�ɻ�е���غ㶨�ɿɵã�
![]() mv02=mg��2R��+
mv02=mg��2R��+ ![]() mv2��
mv2��
��ã�v=4m/s��
��F+mg=m ![]() �ɵã�
�ɵã�
F=22N
��2��
�⣺AB��ײǰA���ٶ�ΪvA���ɻ�е���غ㶨�ɿɵã�
![]() mv02=
mv02= ![]() mvA2
mvA2
��vA=v0=6m/s��
AB��ײ���Թ�ͬ�ٶ�vPǰ����������Ϊ�������ɶ����غ㶨�ɿɵã�
mv0=��m+m��vp
��ã�vP=3m/s��
���ܶ���EK= ![]() ��m+m��vP2=
��m+m��vP2= ![]() ��2��9=9J��
��2��9=9J��
����ÿ����һ�δֲڶ���ʧ�Ļ�е�ܡ�EK=fL=�̣�m+m��gL=0.1��20��0.1=0.2J��
k= ![]() =
= ![]() =45
=45
��3��
�⣺AB���廬����n���⻬������ʧ��������
E��=nE=0.2nJ
��AB��ײ���˶�����n���⻬�εĹ����У��������غ㶨�ɿɵã�
![]() ��m+m��vP2��
��m+m��vP2�� ![]() ��m+m��vAB2=n��E��
��m+m��vAB2=n��E��
�����ã�vAB= ![]() m/s
m/s
����������1���ɻ�е���غ㶨�ɿ����A����Q����ٶȣ�����������ʽ����õ�����С����2���ɻ�е���غ㶨�ɿ����AB��ײǰA���ٶȣ��ٶ���ײ�����ɶ����غ㶨�ɿ����������ٶȣ��������ܶ��ܣ�����Ħ�����������ÿ�������ĵĻ�е�ܣ�������ñ�ֵ����3�����ܹ�������n�Σ�����ÿһ�������ĵ��������������غ����ñ���ʽ��
�����㾫����������Ĺؼ��������������������֪ʶ����������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ�����������Լ��Ի�е���غ㼰�����������⣬�˽���ֻ���������͵��ɵ����������������£����嶯�ܺ��������ܣ����������ܣ������ת��������е�ܵ��������ֲ��䣮

 ��У����ϵ�д�
��У����ϵ�д�