Question

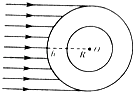
【题目】M、N两颗质量相同的卫星绕地球做匀速圆周运动，其轨道如图所示，已知M卫星的轨道半径大于N卫星的轨道半径，则（ ）

A.M卫星与地球中心连线在相等的时间内转过的角度较大
B.M卫星的机械能大于N卫星的机械能
C.M卫星的速度变化更快
D.M卫星在相同的时间内经过的路程较长

Answer 1

【答案】B
【解析】解：根据万有引力提供向心力得： =ma=mω2r=m = s
A、ω= ，M卫星的角速度小于N卫星的角速度，所以M卫星与地球中心连线在相等的时间内转过的角度较小，故A错误；
B、卫星从低轨道到高轨道需要克服引力做较多的功，所以M卫星的机械能大于N卫星的机械能，故B正确；
C、a= ，M卫星的加速度小于N卫星的加速度，所以M卫星的速度变化更慢，故C错误；
D、v= ，M卫星的线速度小于N卫星的线速度，所以M卫星在相同的时间内经过的路程较短，故D错误；
故选：B．
【考点精析】解答此题的关键在于理解万有引力定律及其应用的相关知识，掌握应用万有引力定律分析天体的运动：把天体的运动看成是匀速圆周运动，其所需向心力由万有引力提供.即 F引=F向；应用时可根据实际情况选用适当的公式进行分析或计算.②天体质量M、密度ρ的估算．