题目内容
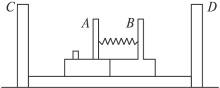
如图9所示，质量均为2.0 kg的物块A、B用轻弹簧相连，放在光滑水平面上，B与竖直墙接触.另一个质量为4.0 kg的物块C以v="3.0" m/s的速度向A运动，C与A碰撞后黏在一起不再分开，它们共同向右运动，并压缩弹簧.求：
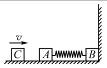
图9
（1）弹簧的最大弹性势能Ep能达到多少?
（2）以后的运动中，B也将会离开竖直墙，那么B离开墙后弹簧的最大弹性势能Ep′是多少.
图9
（1）弹簧的最大弹性势能Ep能达到多少?
（2）以后的运动中，B也将会离开竖直墙，那么B离开墙后弹簧的最大弹性势能Ep′是多少.
（1）12 J （2）3 J
（1）设A和C刚碰后共同速度为vAC，则由动量守恒定律得(mA+mC)vAC=mCv ①
代入数值解得vAC="2" m/s ②
由能量守恒得弹簧的最大弹性势能Ep=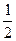
(mA+mC)vAC2="12" J. ③
（2）当A、B、C三者速度相同时弹簧的弹性势能再次达最大，设三者共同速度为vABC,由动量守恒得(mA+mB+mC)vABC=(mA+mC)vAC, ④
解得vABC="1.5" m/s ⑤
由能量守恒得弹簧最大弹性势能Ep′=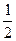(mA+mC)vAC2-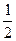(mA+mB+mC)vABC2="3" J. ⑥
代入数值解得vAC="2" m/s ②
由能量守恒得弹簧的最大弹性势能Ep=
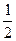(mA+mC)vAC2="12" J. ③（2）当A、B、C三者速度相同时弹簧的弹性势能再次达最大，设三者共同速度为vABC,由动量守恒得(mA+mB+mC)vABC=(mA+mC)vAC, ④
解得vABC="1.5" m/s ⑤
由能量守恒得弹簧最大弹性势能Ep′=
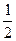(mA+mC)vAC2-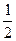(mA+mB+mC)vABC2="3" J. ⑥
练习册系列答案
计算高手系列答案
相关题目
=
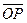（OP1+OP2+…+OP10）
