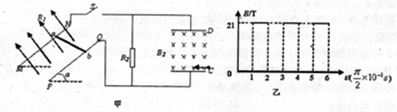
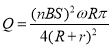题目内容
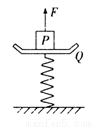
（16分） 一质量为2m的物体P静止于光滑水平地面上，其截面如图所示。图中ab为粗糙的水平面，长度为L；bc为一光滑斜面，斜面和水平面通过与θ和bc均相切的长度可忽略的光滑圆弧连接。现有一质量为m的木块以大小为v0的水平初速度从a点向左运动，在斜面上上升的最大高度为h，返回后在到达a点前与物体P相对静止。重力加速度为g。求：
（1）木块在ab段受到的摩擦力f；
（2）木块最后距a点的距离s。
（1）
（2）
【解析】
试题分析：（1）设木块和物体P共同速度为v,两物体从开始到第一次到达共同速度过程由动量守恒得： 
①
此过程，摩擦力做功损失能量为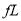
，则根据功能关系有
②
由①②得： ③
（2）木块返回与物体P第二次达到共同速度与第一次相同（动量守恒），全过程能量守恒得：
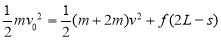④
由②③④得： ⑤
考点：动量守恒定律 功能关系
练习册系列答案
相关题目
