题目内容
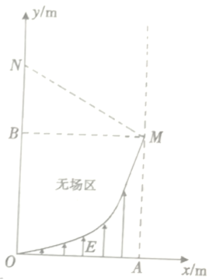
【题目】如图所示,在直角坐标系第一象限中有一匀强电场,该电场区域的曲线边界OM的方程为y=kx2,场强为E。已知坐标系中A点坐标为(xA,0),B点坐标为(0,![]() )在
)在![]() ,y>kx2的范围内,有垂直纸面向里的匀强磁场,磁感应强度为B=
,y>kx2的范围内,有垂直纸面向里的匀强磁场,磁感应强度为B=![]() ,在x轴上OA范围内,均匀分布有大量的正电荷,每个电荷质量为m,带电荷量为q,在电场力作用下由静止开始向上运动不计电荷的重力和电荷间的相互作用力,k为已知量。求:
,在x轴上OA范围内,均匀分布有大量的正电荷,每个电荷质量为m,带电荷量为q,在电场力作用下由静止开始向上运动不计电荷的重力和电荷间的相互作用力,k为已知量。求:
(1)从某一点(x,0)出发的电荷射出电场区后获得的速度;
(2)若要求每个电荷都能在![]() ,y>
,y>![]() 范围内经过磁场区域进行偏转并射出第一象限,求该磁场区域的最小面积;
范围内经过磁场区域进行偏转并射出第一象限,求该磁场区域的最小面积;
(3)若在△BMN区域内存在垂直纸面向里的磁场,且∠BNM=60°。则从BN间射出的电荷中,从x轴出发到射出第一象限的最短时间t为多少?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)在电场中,受电场力作用,有
qE=ma
在电场中的加速位移为
y=kx2
电荷做匀加速直线运动,有
v2=2ay
可得
![]()
(2)从A点出发的电荷,获得最大速度,进入磁场后,有最大半径R,在磁场中有
![]()
根据原题条件可得
R=2xA
几何关系如图所示,可知θ=60°,则磁场区域最小面积为
![]()
(3)由第二问可知,电荷经过y轴时,所有电荷射出的方向与y轴正方向夹角均为60°。当电荷从BN间射出,并与MN相切的时候,此时电荷从出发到离开第一象限所经历的时间最短,可知切点为N点。设该电荷出发点坐标为(x,0)

由R=2x
BN=![]()
可得
![]()
在电场中做匀加速直线运动
qE=ma
![]()
在无场区中,做匀速直线运动
![]()
![]()
在磁场中做匀速圆周运动,运动轨迹对应圆心角为=60°,由
![]()
![]()
则最短时间
t=t1+t2+t3
解得
![]()

练习册系列答案
相关题目