题目内容
一个半圆柱形玻璃体的截面如图13-7-10所示，其中O为圆心，aOb为平面，acb为半圆柱面，玻璃的折射率n=
.一束平行光与aOb面成45°角照到平面上，将有部分光线经过两次折射后由半圆柱面acb射出，试画能有光线射出的那部分区域，并证明这个区域是整个acb弧的一半.
图13-7-10
.一束平行光与aOb面成45°角照到平面上，将有部分光线经过两次折射后由半圆柱面acb射出，试画能有光线射出的那部分区域，并证明这个区域是整个acb弧的一半.图13-7-10
证明：根据折射定律n=sini/sinr知sinr=sini/n=sin45°/=
，可见r=30°，由全反射临界角sinC=
=
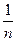知C=45°，由图知①号典型光线有
∠aOd=180°-［C+(90°-r)］=180°-［45°+(90°-30°)］=75°
对②号典型光线有
∠bOe=180°-［C+(90°+r)］=180°-［45°+(90°+30°)］=15°
可见射出区域为∠dOe所对应的圆弧.
因∠dOe=180°-∠aOd-∠bOe=180°-75°-15°=90°.
故这个区域是整个acb弧的一半.
图13-7-11
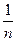=，可见r=30°，由全反射临界角sinC==知C=45°，由图知①号典型光线有∠aOd=180°-［C+(90°-r)］=180°-［45°+(90°-30°)］=75°
对②号典型光线有
∠bOe=180°-［C+(90°+r)］=180°-［45°+(90°+30°)］=15°
可见射出区域为∠dOe所对应的圆弧.
因∠dOe=180°-∠aOd-∠bOe=180°-75°-15°=90°.
故这个区域是整个acb弧的一半.
图13-7-11
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
的玻璃做成内径为R、外径为
的半球形空心球壳，一束平行光射向此半球的外表面，与中心对称轴
平行，试求：
