题目内容
18.取地球的环绕速度为7.9km/s,某行星的质量是地球的8倍,半径是地球的2倍,则此行星的环绕速度为多少?分析 环绕速度的轨道半径为地球的半径,根据万有引力提供向心力$G\frac{mM}{{r}^{2}}=m\frac{{v}^{2}}{r}$,通过轨道半径比和中心天体质量比,求出行星运行的速度和环绕速度的关系,从而得出行星的运行速度.
解答 解:设卫星的质量为m,中心天体的质量为M,半径为R,天体的环绕速度即为卫星星绕天体表面做圆周运动的运行速度,设为v.
即:F向=F引
所以$\frac{GMm}{{R}^{2}}=m\frac{{v}^{2}}{R}$
解得:$v=\sqrt{\frac{GM}{R}}$…①
由题意可得:M行=8M地,R行=2R地…②
由①②得:v行=2v地=15.8km/s
答:此行星的环绕速度为15.8km/s.
点评 本题主要从环绕天体的向心力由万有引力提供$G\frac{mM}{{r}^{2}}=m\frac{{v}^{2}}{r}$,掌握万有引力及环绕速度的意义是正确解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
9.关于两物体间万有引力的大小和它们之间距离的关系,下列说法正确的是( )
| A. | 与距离成正比 | B. | 与距离平方成正比 | ||
| C. | 与距离成反比 | D. | 与距离平方成反比 |
13.在探究平抛运动规律的实验中,下列哪些因素对探究规律有影响( )
| A. | 弧形轨道末端不水平 | B. | 弧形轨道不光滑 | ||
| C. | 实验小球为轻质小球 | D. | 坐标原点不在抛出点 |
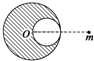 有一质量为M半径为R的密度均匀球体,在距离球心O为2R的地方有一质量为m的质点,现在从M中挖去一半径为$\frac{R}{2}$的球体,如图所示,
有一质量为M半径为R的密度均匀球体,在距离球心O为2R的地方有一质量为m的质点,现在从M中挖去一半径为$\frac{R}{2}$的球体,如图所示,