题目内容
5. 如图所示,A1、A2为两块面积很大、相互平行的金属板,两板间距离为d,以A1板的中点为坐标原点,水平向右和竖直向下分别建立x轴和y轴,在坐标为(0,$\frac{1}{2}d$)的P处有一粒子源,可在坐标平面内向各个方向不断发射同种带电粒子,这些带电粒子的速度大小均为v0,质量为m,带电量为+q,重力忽略不计,不考虑粒子打到板上的反弹,且忽略带电粒子对金属板上电荷分布的影响.
如图所示,A1、A2为两块面积很大、相互平行的金属板,两板间距离为d,以A1板的中点为坐标原点,水平向右和竖直向下分别建立x轴和y轴,在坐标为(0,$\frac{1}{2}d$)的P处有一粒子源,可在坐标平面内向各个方向不断发射同种带电粒子,这些带电粒子的速度大小均为v0,质量为m,带电量为+q,重力忽略不计,不考虑粒子打到板上的反弹,且忽略带电粒子对金属板上电荷分布的影响.(1)若只在A1、A2板间加上恒定电压U0,且A1板电势低于A2板,求粒子打到A1板上的速度大小;
(2)若只在A1、A2板间加上一方向垂直于纸面向外的匀强磁场,磁感应强度为B,且B<$\frac{{2m{v_0}}}{dq}$,求A1板上有
粒子打到的区域范围(用x轴坐标值表示);
(3)在第(2)小题前提下,若在A1、A2板间再加一电压,使初速度垂直指向A1板的粒子打不到A1板,试确定A1、A2板电势的高低以及电压的大小.
分析 (1)带电粒子在电场中加速,由动能定理很容易求出打到A1板的速度大小.
(2)粒子源在P点向各个方向发射速度相同的同种粒子,则这些带电粒子以相同的半径有两板间做匀速圆周运动,求打在A1板上的粒子的范围:先要求出粒子做匀速圆周运动的半径,并与上下板的距离进行对比,再根据粒子旋转的方向,在想象中确定打在最右和最左的位置,但要注意的打在最左的位置分两种情况考虑.
(3)在第二问做匀速圆周运动的基础上在两板间加上电场,这时粒子的运动非常复杂,要使粒子不再打到A1板,应使粒子做曲线运动的曲率半径减小,即使速度v减小,所以应加电场方向向下,即A1板电势高于A2板;恰好不打到A1板,即到达A1板时速度方向与板平行,再在x轴和y轴方向对速度和位移累加,结合动能定理就能求出两板间电压的大小是.
解答  解:(1)粒子运动到A1板,电场力做正功,有:
解:(1)粒子运动到A1板,电场力做正功,有:
$q\frac{U_0}{2}=\frac{1}{2}m{v^2}-\frac{1}{2}m{v_0}^2$
得:$v=\sqrt{{v_0}^2+\frac{{q{U_0}}}{m}}$
(2)磁场中圆周运动,洛伦兹力提供向心力,有:$qvB=m\frac{{{v_0}^2}}{R}$,
解得:$R=\frac{{m{v_0}}}{qB}>\frac{d}{2}$
i 向右偏转打到A1板最远为轨迹恰好与A1板相切的粒子,如图(1)所示,由
几何关系知:${x_右}^2+(R-\frac{d}{2}{)^2}={R^2}$
可得:${x_右}=\sqrt{\frac{{m{v_0}d}}{qB}-\frac{d^2}{4}}$
i i 向左偏转打到A1板最远处对应有两种情况:
易知O2M=$\frac{1}{4}d$,O2N=$\frac{3}{4}d$
情形一:若R<$\frac{3}{4}d$,即$B>\frac{{4m{v_0}}}{3dq}$时,最远处轨道对应为x左,PQ为直径由几何关系知:${(\frac{d}{2})^2}+{x_左}^2={(2R)^2}$
得:${x_左}=\sqrt{\frac{{4{m^2}{v_0}^2}}{{{q^2}{B^2}}}-\frac{d^2}{4}}$
所以,当$B>\frac{{4m{v_0}}}{3dq}$时A1板上有粒子打到的范围x轴坐标是:
$-\sqrt{\frac{4{m}^{2}{{v}_{0}}^{2}}{{q}^{2}{B}^{2}}-\frac{{d}^{2}}{4}}$~$\sqrt{\frac{{m{v_0}d}}{qB}-\frac{d^2}{4}}$
情形二:若R>$\frac{3}{4}d$,即$B<\frac{{4m{v_0}}}{3dq}$时,最远处为轨道与A2相切的粒子打在A1的落点,如图(2)所示
显然仍有x1=$\sqrt{\frac{{m{v_0}d}}{qB}-\frac{d^2}{4}}$
又${(R-d)^2}+{x_2}^2={R^2}$
或${(d-R)^2}+{x_2}^2={R^2}$
得${x_2}=\sqrt{\frac{{2m{v_0}d}}{qB}-{d^2}}$
则x左=x1+x2=$\sqrt{\frac{{m{v_0}d}}{qB}-\frac{d^2}{4}}$+$\sqrt{\frac{{2m{v_0}d}}{qB}-{d^2}}$
所以,当$B<\frac{{4m{v_0}}}{3dq}$时A1板上有粒子打到的范围x轴坐标是:
-($\sqrt{\frac{{m{v_0}d}}{qB}-\frac{d^2}{4}}$+$\sqrt{\frac{{2m{v_0}d}}{qB}-{d^2}}$)~$\sqrt{\frac{{m{v_0}d}}{qB}-\frac{d^2}{4}}$
(3)要使粒子不再打到A1板,应使粒子做曲线运动的曲率半径减小,即使速度v减小,所以应加电场方向向下,
即A1板电势高于A2板;恰好不打到A1板,即到达A1板时速度方向与板平行,设此时速度为v,
$-q\frac{U}{2}=\frac{1}{2}m{v^2}-\frac{1}{2}m{v_0}^2$
对于此时曲线轨迹上任一点在x方向上有$\frac{{△{v_x}}}{△t}=\frac{{q{v_y}B}}{m}=\frac{qB△y}{m△t}$
分别对y方向的位移和x方向的速度累加得:$v=\frac{qdB}{2m}$
得$U=\frac{{m{v_0}^2}}{q}-\frac{{q{B^2}{d^2}}}{4m}$
答:(1)若只在A1、A2板间加上恒定电压U0,且A1板电势低于A2板,求粒子打到A1板上的速度大小$\sqrt{{{v}_{0}}^{2}+\frac{q{U}_{0}}{m}}$.
(2)若只在A1、A2板间加上一方向垂直于纸面向外的匀强磁场,磁感应强度为B,且B<$\frac{{2m{v_0}}}{dq}$,则A1板上有粒子打到的区域范围有两种情况:①当$B>\frac{{4m{v_0}}}{3dq}$时A1板上有粒子打到的范围x轴坐标是:$-\sqrt{\frac{4{m}^{2}{{v}_{0}}^{2}}{{q}^{2}{B}^{2}}-\frac{{d}^{2}}{4}}$~$\sqrt{\frac{{m{v_0}d}}{qB}-\frac{d^2}{4}}$ ②当$B<\frac{{4m{v_0}}}{3dq}$时A1板上有粒子打到的范围x轴坐标是:-($\sqrt{\frac{{m{v_0}d}}{qB}-\frac{d^2}{4}}$+$\sqrt{\frac{{2m{v_0}d}}{qB}-{d^2}}$)~$\sqrt{\frac{{m{v_0}d}}{qB}-\frac{d^2}{4}}$.
(3)在第(2)小题前提下,若在A1、A2板间再加一电压,使初速度垂直指向A1板的粒子打不到A1板,则A1板电势高,且两板电压为$\frac{m{{v}_{0}}^{2}}{q}-\frac{q{B}^{2}{d}^{2}}{4m}$.
点评 本题的难点在于后两问:①求打在A1板上范围,要考虑的因素很多,即有带电粒子的旋转方向及出射方向,其半径与A1和A2板间距大小的关系等.②第三问的要使向A1板射出的粒子打不到A1板,则是洛仑兹力改变其方向的,对于此时曲线轨迹上任一点在x方向上有$\frac{{△{v_x}}}{△t}=\frac{{q{v_y}B}}{m}=\frac{qB△y}{m△t}$,分别对y方向的位移和x方向的速度累加得到时最后平行于A1板的速度即末速度:$v=\frac{qdB}{2m}$,再由动能定理求出两板间的电压.

 如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别挂上小球C和物体B,在B的下端再挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时圆周运动的半径为R,现剪断连接A、B的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别挂上小球C和物体B,在B的下端再挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时圆周运动的半径为R,现剪断连接A、B的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )| A. | 剪断连接A、B的绳子后,小球C的速度不变 | |
| B. | 剪断连接A、B的绳子后,小球C的速度减小 | |
| C. | 剪断连接A、B的绳子后,B、C具有的机械能减小 | |
| D. | 剪断连接A、B的绳子后,B、C具有的机械能增加 |
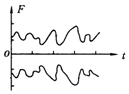 用计算机辅助实验系统做验证牛顿第三定律的实验:用一辆电玩具汽车拖运另一辆无动力的玩具汽车,在两车挂接处装上传感器探头,并把它们的挂钩连在一起.当电玩具汽车通电后拉着另一辆车向前运动时,可以在显示器屏幕上呈现相互作用力随时间变化的图象,如图所示.观察分析两个力传感器的相互作用力随时间变化的曲线,可以得出以下实验结论,其中不正确的是( )
用计算机辅助实验系统做验证牛顿第三定律的实验:用一辆电玩具汽车拖运另一辆无动力的玩具汽车,在两车挂接处装上传感器探头,并把它们的挂钩连在一起.当电玩具汽车通电后拉着另一辆车向前运动时,可以在显示器屏幕上呈现相互作用力随时间变化的图象,如图所示.观察分析两个力传感器的相互作用力随时间变化的曲线,可以得出以下实验结论,其中不正确的是( )| A. | 作用力与反作用力的大小时刻相等 | |
| B. | 作用力与反作用力作用在同一物体上 | |
| C. | 作用力与反作用力方向相反 | |
| D. | 作用力与反作用力大小是同时发生变化的 |
 如图所示,光滑的半球形物体固定在水平地面上,一轻绳一端系在球心正上方的天花板上,另一端系一小球,靠放在半球上,小球处于静止状态.现缓慢减小半球的半径,半球的圆心位置不变,在这个过程中,小球始终与半球接触,则半球对小球的支持力F1和绳对小球的拉力F2的大小变化情况是( )
如图所示,光滑的半球形物体固定在水平地面上,一轻绳一端系在球心正上方的天花板上,另一端系一小球,靠放在半球上,小球处于静止状态.现缓慢减小半球的半径,半球的圆心位置不变,在这个过程中,小球始终与半球接触,则半球对小球的支持力F1和绳对小球的拉力F2的大小变化情况是( )| A. | F1变大,F2变小 | B. | F1变小,F2变大 | ||
| C. | F1变小,F2不变 | D. | F1先变小后变大,F2变小 |
| A. | 晶体的物理性质都是各向异性的 | |
| B. | 露珠呈球状是由于液体表面张力的作用 | |
| C. | 布朗运动是固体分子的运动,它说明分子永不停息地做无规则运动 | |
| D. | 分子热运动是无规则的,但对大量分子的整体而言,它们却表现出规律性 |
| A. | 恒星的质量为$\frac{{4π}^{2}{R}^{3}}{{GT}^{2}}$ | B. | 恒星的第一宇宙速度为$\sqrt{\frac{{v}^{3}T}{2πR}}$ | ||
| C. | 行星的轨道半径为$\frac{{v}^{2}T}{2π}$ | D. | 行星的向心加速度为$\frac{2πv}{T}$ |
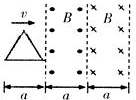 如图所示,一边长为a、电阻为R的等边三角形线框在外力作用下以速度v0匀速穿过宽度均为a的两个匀强磁场区域,线框运动方向与底边平行且与磁场边缘垂直,两磁场磁感应强度的大小均为B,方向相反.以逆时针方向为电流正方向,从图示位置开始线框中感应电流I与沿运动方向的位移s的关系图象可能为( )
如图所示,一边长为a、电阻为R的等边三角形线框在外力作用下以速度v0匀速穿过宽度均为a的两个匀强磁场区域,线框运动方向与底边平行且与磁场边缘垂直,两磁场磁感应强度的大小均为B,方向相反.以逆时针方向为电流正方向,从图示位置开始线框中感应电流I与沿运动方向的位移s的关系图象可能为( )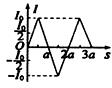
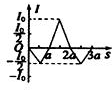

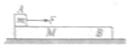 如图所示,物块A和长木板B质量m=1kg,M=2kg,A与B之间动摩擦因数为0.2,开始时A静止在B的左端,B停在光滑的水平地面上,某时刻给A施加F=9N的水平拉力,1s后撤去F,最终A恰好停在B的右端(g取10m/s2)试求:
如图所示,物块A和长木板B质量m=1kg,M=2kg,A与B之间动摩擦因数为0.2,开始时A静止在B的左端,B停在光滑的水平地面上,某时刻给A施加F=9N的水平拉力,1s后撤去F,最终A恰好停在B的右端(g取10m/s2)试求: 如图,地面光滑,质量为m1与m2的物块由轻质弹簧相连,共同以v0=5m/s的速度向右匀速运动,m2与原来静止的质量为m3的物块碰撞后立即黏在一起,已知m1=m2=1kg,m3=4kg,求:
如图,地面光滑,质量为m1与m2的物块由轻质弹簧相连,共同以v0=5m/s的速度向右匀速运动,m2与原来静止的质量为m3的物块碰撞后立即黏在一起,已知m1=m2=1kg,m3=4kg,求: