题目内容
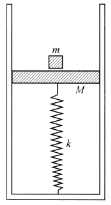
【题目】如图,一内壁光滑、质量为m1=0.1kg、半径为R=0.1m的环形细圆管,固定在一个质量为M=0.5kg的长方体基座上。一质量为m2=0.2kg的小球(可看成质点)在管内做完整的圆周运动,长方体与地面不粘连,且始终相对地面静止。重力加速度记为g=10m/s2,求:

(1)当小球以速率v1=![]() m/s经过最低点时,地面对长方体的支持力大小;
m/s经过最低点时,地面对长方体的支持力大小;
(2)当小球经过最高点时,若长方体对面的压力恰好为零,此时小球的速率v2为多大?
【答案】(1)18N(2)2m/s
【解析】
(1) 设当小球经过最低点时受到圆管对它的支持力为N,小球对圆管的压力为FN,地面对长方体的支持力大小为F支,小球的向心力为:
![]()
由牛顿第三定律可知:
![]()
地面对长方体的支持力大小
F支=FN+Mg+m1g
代入数据联立解得:
F支=18N
(2) 当小球经过最高点时,小球对管道的压力为FN2,小球对圆管的支持力为N2,根据题意得
![]()
根据牛顿第三定律有:
![]()
要使长方体对地面的压力恰好为零,则
N2=Mg+m1g
代入数据联立解得:
v2=2m/s

练习册系列答案
相关题目