题目内容
【题目】如图所示,一气缸放在大气中,大气压![]() ,活塞质量
,活塞质量![]() ,面积
,面积![]() ,活塞下连一弹簧,原长为
,活塞下连一弹簧,原长为![]() ,劲度系数
,劲度系数![]() ,活塞与缸壁都不导热,而活塞与缸壁之间存在摩擦,旦大小恒为
,活塞与缸壁都不导热,而活塞与缸壁之间存在摩擦,旦大小恒为![]() .假设摩擦产生的热有一半被活塞下的气体吸收,活塞下有
.假设摩擦产生的热有一半被活塞下的气体吸收,活塞下有![]() 的理想单原子气体,初态
的理想单原子气体,初态![]() ,温度
,温度![]() ℃,固定活塞,在活塞上放上质量为
℃,固定活塞,在活塞上放上质量为![]() 的木块后,释放活塞(
的木块后,释放活塞(![]() 取
取![]() ),木块脱离活塞后不再回来,求:
),木块脱离活塞后不再回来,求:
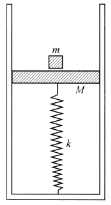
(1)活塞上升达到的最大高度(相对于气缸底部);
(2)活塞上升达到最大高度时气体的状态参量,即压强、体积、温度
【答案】(1)![]() (2) 气体的压强
(2) 气体的压强![]() ,体积
,体积![]() ,温度
,温度![]() ℃.
℃.
【解析】
(1)设活塞至缸底的距离为![]() ,以
,以![]() 、
、![]() 、
、![]() 表示气体的状态参量,则有
表示气体的状态参量,则有![]() ,
,
即![]() . ①
. ①
依题意,由热力学第一定律有![]() . ②
. ②
由①②两式可得![]() . ③
. ③
对上式考虑到初始条件,有![]() ,即有
,即有![]() .
.
此式说明,气体在变化过程中,其压强保持不变,为等压道程.
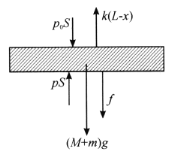
对活塞与木块整体进行受力分析,其受力如图所示,有活塞在平衡位置时有
![]() ,
,
解得![]() . ④
. ④
活塞在分离木块位置时,活塞的加速度为![]() ,此时应有
,此时应有![]() ,
,
解得![]() . ⑤
. ⑤
由于![]() 、
、![]() 、
、![]() 、
、![]() 均为恒力,则系统的运动是在弹力作用的简谐运动,且
均为恒力,则系统的运动是在弹力作用的简谐运动,且
![]() (木块脱离前),
(木块脱离前),
对气体的初态进行分析,有![]() ,解得
,解得![]() .
.
所以,木块脱离前活塞振动的振幅为![]() .
.
则活塞用![]() 表示的振动方程为
表示的振动方程为![]() .
.
于是![]() ,
,
代入![]() ,得
,得![]() ,
,![]() .
.
此后,振动的平衡位置发生变化,平衡位置满足
![]() ,解得
,解得![]() .
.
且新的振幅满足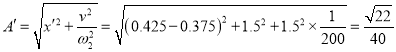 .
.
故振动方程为![]() .
.
代入![]() 时,
时,![]() ,得
,得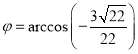 .
.
又![]() ,
,
当![]() 时,
时,![]() .
.
此时![]() ,则活塞相对于气缸底部上升到达的总高度为
,则活塞相对于气缸底部上升到达的总高度为
![]() .
.
(2)活塞上升达到最大高度时,
气体的压强![]() ,
,
体积![]() ,
,
温度![]() ℃.
℃.
说明:对于本题的解答,如不能作出气体的变化过程是等压变化,那么,我们也许会经历如下的解答过程.
设开始时,弹簧的长度为![]() ,则由克拉珀龙方程,有
,则由克拉珀龙方程,有![]() ,解得
,解得![]() .
.
释放活塞时,有![]() ,即活塞会向上运动.
,即活塞会向上运动.
木块脱离活塞时,其应具有向下的加速度![]() ,设此时弹簧的长度为
,设此时弹簧的长度为![]() ,且
,且![]() ,气体的压强为
,气体的压强为![]() ,温度为
,温度为![]() ,所以,对活塞有
,所以,对活塞有![]() .
.
对气体有![]() .
.
对系统有![]()
![]() .
.
此后,活塞继续上升,上升到最大高度时,设弹簧的长度为![]() ,且
,且![]() ,气体的压强为
,气体的压强为![]() ,温度为
,温度为![]() ,所以,对系统有
,所以,对系统有![]()
![]() .
.
对气体有![]() .
.
至此,我们应该进入到解方程的阶段,但基本上会是无功而返.