题目内容
 (2013?福建模拟)如图1所示,质量足够大、截面是直角梯形的物块静置在光滑水平地面上,其两个侧面恰合与两个固定在地面上的压力传感器X和Y相接触,图AB高H=0.3m,AD长L=0.5m,斜面倾角θ=37°有一质量m=1kg的小物块p(图中未画出),它与斜面的动磨擦因数μ可以通过更换斜面的材料进行调节,调节范围是0≤μ≤1,取sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2.
(2013?福建模拟)如图1所示,质量足够大、截面是直角梯形的物块静置在光滑水平地面上,其两个侧面恰合与两个固定在地面上的压力传感器X和Y相接触,图AB高H=0.3m,AD长L=0.5m,斜面倾角θ=37°有一质量m=1kg的小物块p(图中未画出),它与斜面的动磨擦因数μ可以通过更换斜面的材料进行调节,调节范围是0≤μ≤1,取sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2.(1)在A点给P一个沿斜面向上的初速度v0=3m/s,使之恰好能到达D点,求此时动摩擦因数μ的值;
(2)在第(1)问中若μ=0.5,求p落地时的动能;
(3)对于不同的μ,每次都在D点给p一个沿斜面向下足够大的初速度以保证它能滑离斜面.
在p沿斜面下滑过程中,通过压力传感器能读出X或Y对大物块的水平压力F,取水平向左为正方向,试写出F随μ变化的关系表达式,并在坐标系(图2)中画出其函数图象.
分析:(1)对A到D过程分析,由动能定理可求得动摩擦因数的值;
(2)设上滑的位移为S,由动能定理可求得上滑的高度;对全程由动能定理可求得落地时的动能;
(3)对梯形物块进行受力分析,由共点力的平衡条件可求得F的表达式,根据表达式可画出图象.
(2)设上滑的位移为S,由动能定理可求得上滑的高度;对全程由动能定理可求得落地时的动能;
(3)对梯形物块进行受力分析,由共点力的平衡条件可求得F的表达式,根据表达式可画出图象.
解答:解:(1)小物块从A运动到D时速度为零,由动能定理得:
-(mgsinθ+μmgcosθ)L=
mv02
代入数据解得:μ=
;
(2)设小物块沿斜面上滑位移为S时速度为零,则由动能定理:
-(mgsinθ+μmgcosθ)s=0-
mv02;
代入数据解得:S=0.45m;
设落地时P的动能为EK,则由动能定理:
mgH-μmgcosθ?2S=EK-
mv02
代入数据解得:EK=3.9J;
(3)P在斜面上下滑的过程中,梯形物块的受力如图所示,设梯形物体块的质量为M.
由平衡条件可得:F+Nsinθ=fcosθ;
N=mgcosθ
f=μN=μmgcosθ;
联立以上三式,代入数据得:F=6.4μ-4.8;
答:(1)动摩擦因数为
;(2)落地时的动能为3.9J;(3)图象如下图.

-(mgsinθ+μmgcosθ)L=
| 1 |
| 2 |
代入数据解得:μ=
| 3 |
| 8 |
(2)设小物块沿斜面上滑位移为S时速度为零,则由动能定理:
-(mgsinθ+μmgcosθ)s=0-
| 1 |
| 2 |
代入数据解得:S=0.45m;
设落地时P的动能为EK,则由动能定理:
mgH-μmgcosθ?2S=EK-
| 1 |
| 2 |
代入数据解得:EK=3.9J;
(3)P在斜面上下滑的过程中,梯形物块的受力如图所示,设梯形物体块的质量为M.
由平衡条件可得:F+Nsinθ=fcosθ;
N=mgcosθ
f=μN=μmgcosθ;
联立以上三式,代入数据得:F=6.4μ-4.8;
答:(1)动摩擦因数为
| 3 |
| 8 |

点评:本题考查动能定理的应用,在解题时要正确进行受力分析,并且合理选择研究过程,找出正确的物理规律求解.

练习册系列答案
相关题目
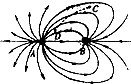 (2013?福建模拟)如图所示为A、B两点电荷形成的电场线分布图,一带正电粒子仅在电场力作用下从C点运动到D点,轨迹如图虚线所示,则下列说法正确的是( )
(2013?福建模拟)如图所示为A、B两点电荷形成的电场线分布图,一带正电粒子仅在电场力作用下从C点运动到D点,轨迹如图虚线所示,则下列说法正确的是( ) (2013?福建模拟)图甲是某燃气炉点火装置的原理图,转换器将直流电压转换为图乙所示的正弦交变电压,并加在一理想变压器的原线圈上,变压器原、副线圈的匝数分别为n1、n2,交流电压表为理想电表.当变压器副线圈电压的瞬时值大于5000V时,就会在钢针和金属板间引发电火花进而点燃气体.以下判断正确的是( )
(2013?福建模拟)图甲是某燃气炉点火装置的原理图,转换器将直流电压转换为图乙所示的正弦交变电压,并加在一理想变压器的原线圈上,变压器原、副线圈的匝数分别为n1、n2,交流电压表为理想电表.当变压器副线圈电压的瞬时值大于5000V时,就会在钢针和金属板间引发电火花进而点燃气体.以下判断正确的是( ) (2013?福建模拟)如图所示,一简谐横波以速度v沿x轴正方向传播,t=0时传播到坐标原点,此质点正从平衡位置以速度v0向下振动,已知质点的振幅为A,振动角频率为
(2013?福建模拟)如图所示,一简谐横波以速度v沿x轴正方向传播,t=0时传播到坐标原点,此质点正从平衡位置以速度v0向下振动,已知质点的振幅为A,振动角频率为