题目内容
 (2013?福建模拟)如图所示,一简谐横波以速度v沿x轴正方向传播,t=0时传播到坐标原点,此质点正从平衡位置以速度v0向下振动,已知质点的振幅为A,振动角频率为ω(ω=
(2013?福建模拟)如图所示,一简谐横波以速度v沿x轴正方向传播,t=0时传播到坐标原点,此质点正从平衡位置以速度v0向下振动,已知质点的振幅为A,振动角频率为ω(ω=| 2π |
| T |
| 3 |
| 4 |
分析:根据λ=vT,计算出
λ处质点振动相对于原点滞后的时间,然后数学知识得到振动方程.
| 3 |
| 4 |
解答:解:根据λ=vT,得:T=
,则波从原点传播到
λ所用的时间t=
,
t=0时,原点处的质点向下振动,则其振动方程为y=-Asinωt,
x轴上横坐标为
λ处质点振动比原点滞后t=
,
结合数学知识知其振动方程为:y=-Asinω(t-
)
故选:B.
| λ |
| v |
| 3 |
| 4 |
| 3λ |
| 4v |
t=0时,原点处的质点向下振动,则其振动方程为y=-Asinωt,
x轴上横坐标为
| 3 |
| 4 |
| 3λ |
| 4v |
结合数学知识知其振动方程为:y=-Asinω(t-
| 3λ |
| 4v |
故选:B.
点评:若为正弦函数,振动方程的通式为y=Asinω(t-t0),t0为质点滞后原点处质点的时间.

练习册系列答案
相关题目
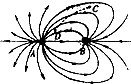 (2013?福建模拟)如图所示为A、B两点电荷形成的电场线分布图,一带正电粒子仅在电场力作用下从C点运动到D点,轨迹如图虚线所示,则下列说法正确的是( )
(2013?福建模拟)如图所示为A、B两点电荷形成的电场线分布图,一带正电粒子仅在电场力作用下从C点运动到D点,轨迹如图虚线所示,则下列说法正确的是( ) (2013?福建模拟)图甲是某燃气炉点火装置的原理图,转换器将直流电压转换为图乙所示的正弦交变电压,并加在一理想变压器的原线圈上,变压器原、副线圈的匝数分别为n1、n2,交流电压表为理想电表.当变压器副线圈电压的瞬时值大于5000V时,就会在钢针和金属板间引发电火花进而点燃气体.以下判断正确的是( )
(2013?福建模拟)图甲是某燃气炉点火装置的原理图,转换器将直流电压转换为图乙所示的正弦交变电压,并加在一理想变压器的原线圈上,变压器原、副线圈的匝数分别为n1、n2,交流电压表为理想电表.当变压器副线圈电压的瞬时值大于5000V时,就会在钢针和金属板间引发电火花进而点燃气体.以下判断正确的是( )