题目内容
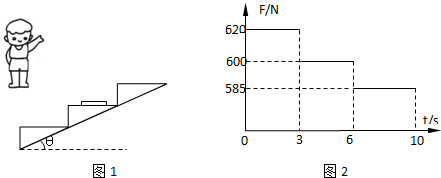
(1)①某同学设计了一个探究小车的加速度a与小车所受拉力F及质量m关系的实验,图中(甲)为实验装置简图.他想用钩码的重力表示小车受到的合外力,为了减小这种做法带来的实验误差,你认为下列说法中正确的是 (选填字母代号).
A.实验时要平衡摩擦力 B.实验时不需要平衡摩擦力
C.钩码的重力要远小于小车的总重力 D.实验进行时应先释放小车再接通电源
②如图(乙)所示是某次实验中得到的一条纸带,其中A、B、C、D、E是计数点(每打5个点取一个计数点),其中L1=3.07cm,L2=12.38cm,L3=27.87cm,L4=49.62cm.则打C点时小车的速度为 m/s,小车的加速度是 m/s2.(计算结果均保留三位有效数字)
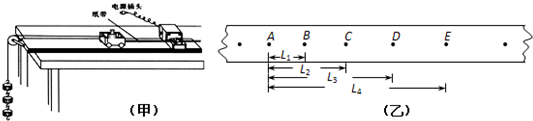
(2)①某实验小组在“测定金属电阻率”的实验过程中,正确操作获得金属丝的直径以及电流表、电压表的读数如图所示,则它们的读数值依次是 mm、 A、 V.
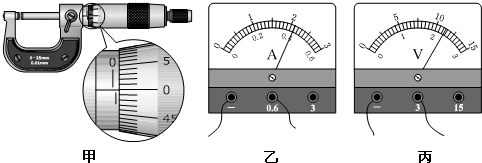
②已知实验中所用的滑动变阻器阻值范围为0~10Ω,电流表内阻约几欧,电压表内阻约20kΩ,电源为干电池(不宜在长时间、大功率状况下使用),电源电动势E=4.5V,内阻较小.则以下电路图中, (选填字母代号)电路为本次实验应当采用的最佳电路,但用此最佳电路测量的金属丝电阻仍然会比真实值偏 (选填“大”或“小”).
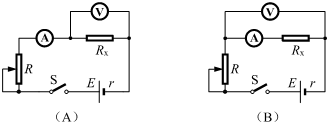
③若已知实验所用的电流表内阻的准确值RA=2.0Ω,那么测量金属丝电阻Rx的最佳电路应是图中的 电路(选填字母代号).此时测得电流为I、电压为U,则金属丝电阻Rx= ( 用题中字母代号表示).
A.实验时要平衡摩擦力 B.实验时不需要平衡摩擦力
C.钩码的重力要远小于小车的总重力 D.实验进行时应先释放小车再接通电源
②如图(乙)所示是某次实验中得到的一条纸带,其中A、B、C、D、E是计数点(每打5个点取一个计数点),其中L1=3.07cm,L2=12.38cm,L3=27.87cm,L4=49.62cm.则打C点时小车的速度为

(2)①某实验小组在“测定金属电阻率”的实验过程中,正确操作获得金属丝的直径以及电流表、电压表的读数如图所示,则它们的读数值依次是

②已知实验中所用的滑动变阻器阻值范围为0~10Ω,电流表内阻约几欧,电压表内阻约20kΩ,电源为干电池(不宜在长时间、大功率状况下使用),电源电动势E=4.5V,内阻较小.则以下电路图中,

③若已知实验所用的电流表内阻的准确值RA=2.0Ω,那么测量金属丝电阻Rx的最佳电路应是图中的
分析:(1)探究加速度与拉力、质量间的关系,平衡摩擦力后,在钩码质量远小于小车质量时,可以认为小车受到的拉力等于钩码重力;实验时应先接通电源,再放开小车;
做匀变速直线运动的物体在某段时间内的平均速度等于该时间中间时刻的瞬时速度;由△x=at2可以求出加速度.
(2)①螺旋测微器固定刻度示数与可动刻度示数之和是螺旋测微器的示数;由图示电表确定电表量程与分度值,读出电表示数;
②根据待测电阻与电表内阻间的关系确定电流表的接法,然后选择实验电路,根据实验电路分析实验误差;
③在已知电流表内阻的情况下,可以采用电流表内接法,由串联电路特点及欧姆定律可以求出待测电阻阻值.
做匀变速直线运动的物体在某段时间内的平均速度等于该时间中间时刻的瞬时速度;由△x=at2可以求出加速度.
(2)①螺旋测微器固定刻度示数与可动刻度示数之和是螺旋测微器的示数;由图示电表确定电表量程与分度值,读出电表示数;
②根据待测电阻与电表内阻间的关系确定电流表的接法,然后选择实验电路,根据实验电路分析实验误差;
③在已知电流表内阻的情况下,可以采用电流表内接法,由串联电路特点及欧姆定律可以求出待测电阻阻值.
解答:解:(1)①探究小车的加速度a与小车所受拉力F及质量m关系的实验中,
A、实验时需要平衡摩擦力,平衡摩擦力后,小车受到的拉力等于钩码的重力,故A正确,B错误;
C、当钩码的重力要远小于小车的总重力时,小车受到的拉力等于钩码重力,故C正确;
D、实验进行时应先接通电源再放开小车,故D错误;故选AC.
②计数点间的时间间隔t=0.02s×5=0.1s,vC=
=
=
=124cm/s=1.24m/s;
加速度a=
=
=
≈623cm/s2=6.23m/s2;
(2)①由图甲所示可知,螺旋测微器固定刻度示数是0.5mm,可动刻度示数是49.9×0.01mm=0.499mm,则螺旋测微器示数为0.5mm+0.499mm=0.999mm;
由图乙所示电流表可知,电流表量程是0~0.6A,分度值是0.02A,示数为0.42A;电压表量程是0~3V,分度值是0.1V,示数为2.25V;
②待测电阻阻值R=
=
≈5.4Ω,电流表内阻约几欧,电压表内阻约20kΩ,相对来说电压表内阻远大于待测电阻值阻值,
电流表应采用外接法,应选A所示实验电路;由于电压表的分流作用,所测电流偏大,由欧姆定律可知,待测电阻测量值小于真实值.
③已知实验所用的电流表内阻的准确值RA=2.0Ω,那么测量金属丝电阻Rx的最佳电路应是图中的B电路;
由欧姆定律可得:RA+RX=
,RX=
-RA;
故答案为:(1)①AC;②1.24,6.22;(2)①0.999,0.42,2.25;②A,小;③B,
-RA.
A、实验时需要平衡摩擦力,平衡摩擦力后,小车受到的拉力等于钩码的重力,故A正确,B错误;
C、当钩码的重力要远小于小车的总重力时,小车受到的拉力等于钩码重力,故C正确;
D、实验进行时应先接通电源再放开小车,故D错误;故选AC.
②计数点间的时间间隔t=0.02s×5=0.1s,vC=
| BD |
| 2t |
| L3-L1 |
| 2t |
| 27.87cm-3.07cm |
| 2×01s |
加速度a=
| DE-AB |
| 3t2 |
| L4-L3-L1 |
| 3t2 |
| 49.62cm-27.87cm-3.07cm |
| 3×(0.1s)2 |
(2)①由图甲所示可知,螺旋测微器固定刻度示数是0.5mm,可动刻度示数是49.9×0.01mm=0.499mm,则螺旋测微器示数为0.5mm+0.499mm=0.999mm;
由图乙所示电流表可知,电流表量程是0~0.6A,分度值是0.02A,示数为0.42A;电压表量程是0~3V,分度值是0.1V,示数为2.25V;
②待测电阻阻值R=
| U |
| I |
| 2.25V |
| 0.42A |
电流表应采用外接法,应选A所示实验电路;由于电压表的分流作用,所测电流偏大,由欧姆定律可知,待测电阻测量值小于真实值.
③已知实验所用的电流表内阻的准确值RA=2.0Ω,那么测量金属丝电阻Rx的最佳电路应是图中的B电路;
由欧姆定律可得:RA+RX=
| U |
| I |
| U |
| I |
故答案为:(1)①AC;②1.24,6.22;(2)①0.999,0.42,2.25;②A,小;③B,
| U |
| I |
点评:螺旋测微器固定刻度与可动刻度所示之和是螺旋测微器的示数,螺旋测微器需要估读;对电流表与电压表读数时,要先确定电表的量程与分度值,然后读数,读数时视线要与电表刻度线垂直.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目

 的量程为2V,内阻约为2k.现要较准确测量其内阻Rv,实验室提供的器材如下:
的量程为2V,内阻约为2k.现要较准确测量其内阻Rv,实验室提供的器材如下:
 ,量程S v,内阻约为5kΩ
,量程S v,内阻约为5kΩ 两端的电压和流过电压表
两端的电压和流过电压表 的电流,再计算出Rv.该方案实际上不可行,其最主要的原因是
的电流,再计算出Rv.该方案实际上不可行,其最主要的原因是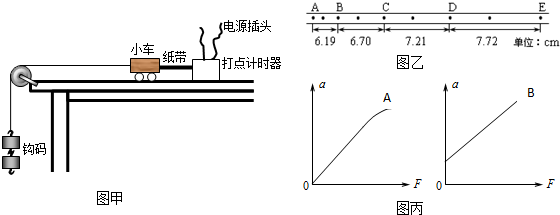
 某同学设计了如图所示的电路测电源电动势E及电阻R1的阻值.实验器材有:待测电源E,待测电阻R1,定值电阻R2,电流表A(量程为0.6A,内阻不计),电阻箱R(0-99.99Ω),单刀单掷开关S1,单刀双掷开关
某同学设计了如图所示的电路测电源电动势E及电阻R1的阻值.实验器材有:待测电源E,待测电阻R1,定值电阻R2,电流表A(量程为0.6A,内阻不计),电阻箱R(0-99.99Ω),单刀单掷开关S1,单刀双掷开关