题目内容
6.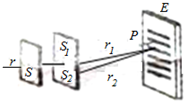 如图所示,把氦-氖激光器及双缝干涉仪放在特制的折射率为$\frac{4}{3}$的介质装置中,若在屏上得到一套干涉条纹,事先测得双缝到屏间的距离为10.8m,双缝间的距离为0.44mm.现测得7条亮条纹间的距离为9cm,则此激光在真空中的波长为8.1×10-7m.
如图所示,把氦-氖激光器及双缝干涉仪放在特制的折射率为$\frac{4}{3}$的介质装置中,若在屏上得到一套干涉条纹,事先测得双缝到屏间的距离为10.8m,双缝间的距离为0.44mm.现测得7条亮条纹间的距离为9cm,则此激光在真空中的波长为8.1×10-7m.
分析 根据干涉条纹的宽度公式:△x=$\frac{L}{d}$λ,结合题意条件,即可求解光在介质中的波长,再根据v=$\frac{c}{n}$与v=λf,即可求解.
解答 解:根据干涉条纹宽度公式:△x=$\frac{L}{d}$λ;
△x=9.0 cm×$\frac{1}{7-1}$=1.5×10-2 m.
用△x=1.5×10-2 m
及d=0.44 mm=0.44×10-3 m,
L=10.8 m,
代入λ=d$\frac{△x}{L}$
可得:λ=$\frac{4.4×1.5}{10.8}×1{0}^{-6}$=6.1×10-7 m.
根据v=$\frac{c}{n}$与v=λf,则有$\frac{{λ}_{真}}{{λ}_{水}}=\frac{\frac{c}{f}}{\frac{c}{nf}}$=n;
因此激光在真空中的波长为 λ真=$\frac{4}{3}×$6.1×10-7 m=8.1×10-7 m
故答案为:8.1×10-7.
点评 考查干涉条纹间距公式,注意△x与7条亮条纹的关系,同时注意各量的单位统一,并掌握v=$\frac{c}{n}$与v=λf,公式的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
16.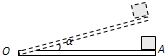 如图所示,长为L的长木板水平放置,在木板的A端放置一个质量为m的小物块,现缓慢地抬高A端,使木板以左端O点为轴转动,当木板转到与水平面的夹角为α时小物块开始滑动,此时停止转动木板,小物块滑到底端的速度为v,则在整个过程中( )
如图所示,长为L的长木板水平放置,在木板的A端放置一个质量为m的小物块,现缓慢地抬高A端,使木板以左端O点为轴转动,当木板转到与水平面的夹角为α时小物块开始滑动,此时停止转动木板,小物块滑到底端的速度为v,则在整个过程中( )
 如图所示,长为L的长木板水平放置,在木板的A端放置一个质量为m的小物块,现缓慢地抬高A端,使木板以左端O点为轴转动,当木板转到与水平面的夹角为α时小物块开始滑动,此时停止转动木板,小物块滑到底端的速度为v,则在整个过程中( )
如图所示,长为L的长木板水平放置,在木板的A端放置一个质量为m的小物块,现缓慢地抬高A端,使木板以左端O点为轴转动,当木板转到与水平面的夹角为α时小物块开始滑动,此时停止转动木板,小物块滑到底端的速度为v,则在整个过程中( )| A. | 支持力对小物块做功为零 | |
| B. | 支持力对小物块做功为mgLsinα | |
| C. | 静摩擦力对小物块做功为mgLsinα | |
| D. | 滑动摩擦力对小物块做功为$\frac{1}{2}$mv2-mgLsinα |
14.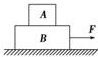 如图所示,一块长木板B放在光滑的水平面上,在B上放一物体A,现以恒定的外力拉B,由于A,B间摩擦力的作用,A将在B上滑动,以地面为参考系,A和B都向前移动一段距离,在此过程中( )
如图所示,一块长木板B放在光滑的水平面上,在B上放一物体A,现以恒定的外力拉B,由于A,B间摩擦力的作用,A将在B上滑动,以地面为参考系,A和B都向前移动一段距离,在此过程中( )
 如图所示,一块长木板B放在光滑的水平面上,在B上放一物体A,现以恒定的外力拉B,由于A,B间摩擦力的作用,A将在B上滑动,以地面为参考系,A和B都向前移动一段距离,在此过程中( )
如图所示,一块长木板B放在光滑的水平面上,在B上放一物体A,现以恒定的外力拉B,由于A,B间摩擦力的作用,A将在B上滑动,以地面为参考系,A和B都向前移动一段距离,在此过程中( )| A. | 外力F做的功等于A和B动能的增量 | |
| B. | B对A的摩擦力所做的功大于A的动能的增量 | |
| C. | A对B的摩擦力所做的功大小等于B对A的摩擦力所做的功大小 | |
| D. | 外力F对B做的功等于B的动能的增量与B克服摩擦力所做的功之和 |
11.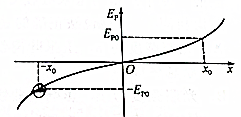 一个带负电的粒子只在电场力的作用下由电场中的-x0位置运动到x0位置时,速度恰好为零,粒子的电势能随位置变化关系如图所示,则下列说法正确的是( )
一个带负电的粒子只在电场力的作用下由电场中的-x0位置运动到x0位置时,速度恰好为零,粒子的电势能随位置变化关系如图所示,则下列说法正确的是( )
 一个带负电的粒子只在电场力的作用下由电场中的-x0位置运动到x0位置时,速度恰好为零,粒子的电势能随位置变化关系如图所示,则下列说法正确的是( )
一个带负电的粒子只在电场力的作用下由电场中的-x0位置运动到x0位置时,速度恰好为零,粒子的电势能随位置变化关系如图所示,则下列说法正确的是( )| A. | 粒子在-x0和x0两位置之间做往复运动 | |
| B. | 粒子从-x0位置运动到x0位置的过程中动能先增大后减小 | |
| C. | 粒子在-x0位置处动能为2EPO | |
| D. | 粒子从-x0位置运动到x0位置的过程中加速度先增大后减小 |
18.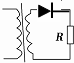 一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压u1=220$\sqrt{2}$sin100πtV 副线圈所接电路如图所示,D为二极管,它两端加上正向电压时,其电阻等于零;加上反向电压时,其电阻无限大,电阻R=10Ω,下列说法正确的是( )
一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压u1=220$\sqrt{2}$sin100πtV 副线圈所接电路如图所示,D为二极管,它两端加上正向电压时,其电阻等于零;加上反向电压时,其电阻无限大,电阻R=10Ω,下列说法正确的是( )
 一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压u1=220$\sqrt{2}$sin100πtV 副线圈所接电路如图所示,D为二极管,它两端加上正向电压时,其电阻等于零;加上反向电压时,其电阻无限大,电阻R=10Ω,下列说法正确的是( )
一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压u1=220$\sqrt{2}$sin100πtV 副线圈所接电路如图所示,D为二极管,它两端加上正向电压时,其电阻等于零;加上反向电压时,其电阻无限大,电阻R=10Ω,下列说法正确的是( )| A. | 原线圈输入功率为24.2W | B. | 流过电阻R的电流有效值为1.1A | ||
| C. | 原线圈两端电压有效值为220 $\sqrt{2}$V | D. | 交流电的频率为100Hz |
15.以下说法中正确的是( )
| A. | 无线电波、可见光、红外线、紫外线、X射线的波长逐渐减小 | |
| B. | 折射率越大,介质对光的偏折本领越大 | |
| C. | 海市蜃楼产生是因为光的衍射现象 | |
| D. | 相机镜头上的增透膜利用的是光的偏振现象,增加了透射光的能量,让成像更清晰 |
14.通电直导线与矩形金属线框位于同一平面内,如图所示.为使线框产生图示方向的感应电流,可( )
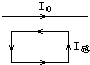

| A. | 使导线水平旋转90° | B. | 使线框平行导线向左移动 | ||
| C. | 使线框远离导线移动 | D. | 使导线中电流I0增强 |
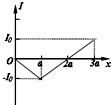
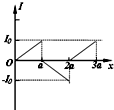
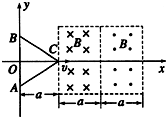 如图所示,两个垂直纸面的匀强磁场方向相反.磁感应强度的大小均为B,磁场区域的宽度为a,一正三角形(高度为a)导线框ABC从图示位置沿图示方向匀速穿过两磁场区域,以逆时针方向为电流的正方向,在下图中感应电流I与线框移动距离x的关系图的是( )
如图所示,两个垂直纸面的匀强磁场方向相反.磁感应强度的大小均为B,磁场区域的宽度为a,一正三角形(高度为a)导线框ABC从图示位置沿图示方向匀速穿过两磁场区域,以逆时针方向为电流的正方向,在下图中感应电流I与线框移动距离x的关系图的是( )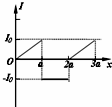

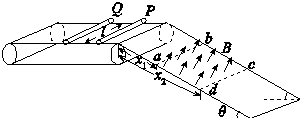 如图所示,一水平匀速运动的传送带,右侧通过小圆弧连接两根直光滑金属导轨,金属导轨与水平面成θ=30°角,传送带与导轨宽度均为L=1m.沿导轨方向距导轨顶端x1=0.7m到x2=2.4m之间存在垂直于导轨平面向上的匀强磁场区域abcd,ab、cd垂直于平行导轨,磁感应强度B=1T.将质量均为m=0.1kg的导体棒P、Q相隔△t=0.2s分别从传送带的左端自由释放,两导体棒与传送带间的动摩擦因数均为μ=0.1,两棒到达传送带右端时已与传送带共速.导体棒P、Q在导轨上运动时,始终与导轨垂直且接触良好,P棒进入磁场时刚好做匀速运动,Q棒穿出磁场时速度为$2\sqrt{6}$m/s.导体棒P、Q的电阻均为R=4Ω,导轨电阻不计,g取10m/s2.
如图所示,一水平匀速运动的传送带,右侧通过小圆弧连接两根直光滑金属导轨,金属导轨与水平面成θ=30°角,传送带与导轨宽度均为L=1m.沿导轨方向距导轨顶端x1=0.7m到x2=2.4m之间存在垂直于导轨平面向上的匀强磁场区域abcd,ab、cd垂直于平行导轨,磁感应强度B=1T.将质量均为m=0.1kg的导体棒P、Q相隔△t=0.2s分别从传送带的左端自由释放,两导体棒与传送带间的动摩擦因数均为μ=0.1,两棒到达传送带右端时已与传送带共速.导体棒P、Q在导轨上运动时,始终与导轨垂直且接触良好,P棒进入磁场时刚好做匀速运动,Q棒穿出磁场时速度为$2\sqrt{6}$m/s.导体棒P、Q的电阻均为R=4Ω,导轨电阻不计,g取10m/s2.