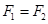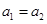题目内容
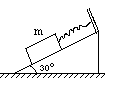
如图12所示，足够长的斜面倾角θ=37°，一物体以v0=12m/s的初速度，从斜面A点沿斜面向上运动，加速度大小为a=8.0m／s2．已知重力加速度g=10m/s2，sin 37°= 0.6，cos 37°=0.8．求：
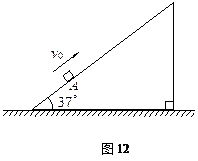（1）物体沿斜面上滑的最大距离s；
（2）物体与斜面间的动摩擦因数μ；
（3）物体沿斜面到达最高点后返回下滑至A点时的速度大小v．
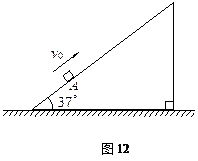（1）物体沿斜面上滑的最大距离s；（2）物体与斜面间的动摩擦因数μ；
（3）物体沿斜面到达最高点后返回下滑至A点时的速度大小v．
（1）9m（2）0.25（3）8.5（m／s）
熟练掌握牛顿第二定律和匀加速直线运动规律是是求解此题的关键。另外就是对物体的受力和运动情景要分析准确、到位，计算过程中要倍加细心和严谨，问题即可得到解决。
（1）根据运动学公式 2as ＝v 解得 s＝ ＝＝ 9m
（2）根据牛顿第二定律 mg sin 37°＋μmg cos 37°＝ma
解得 μ＝＝－ tan 37°
＝－＝ 0.25
（3）设沿斜面下滑时的加速度为a′，根据牛顿第二定律
mg sin 37°－μmg cos 37°＝ma′
解得a′＝g sin 37°－μg cos 37°
＝g（sin 37°－μ cos 37°）
＝10×（0.6－0.8×）＝ 4（m／s2）
根据运动学公式 2a′s ＝v2
解得 v＝＝＝6＝8.5（m／s）
（1）根据运动学公式 2as ＝v 解得 s＝ ＝＝ 9m
（2）根据牛顿第二定律 mg sin 37°＋μmg cos 37°＝ma
解得 μ＝＝－ tan 37°
＝－＝ 0.25
（3）设沿斜面下滑时的加速度为a′，根据牛顿第二定律
mg sin 37°－μmg cos 37°＝ma′
解得a′＝g sin 37°－μg cos 37°
＝g（sin 37°－μ cos 37°）
＝10×（0.6－0.8×）＝ 4（m／s2）
根据运动学公式 2a′s ＝v2
解得 v＝＝＝6＝8.5（m／s）
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
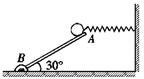
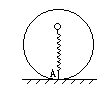
=0.2，盒内存在着竖直向上的匀强电场，场强大小E=2mg/q，盒外没有电场．盒子的上表面开有一系列略大于小球的小孔，孔间距满足一定的关系，使得小球进出盒子的过程中始终不与盒子接触．当小球A以1m/s的速度从孔1进入盒子的瞬间，盒子B恰以v1="6" m/s的初速度向右滑行．已知盒子通过电场对小球施加的作用力与小球通过电场对盒子施加的作用力大小相等、方向相反．设盒子足够长，取重力加速度g=10m/s2，小球恰能顺次从各个小孔进出盒子，且不与盒子底部相碰。试求：
进入盒子至盒子停止运动的过程中，盒子通过的总路程．
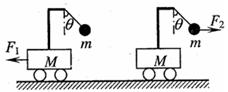
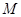，放在光滑的水平面上，小车横梁上用细线各悬挂一质量为
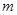的小球，若分别施加水平恒力
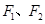，整个装置分别以加速度
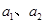做匀加速运动，但两条细线与竖直方向夹角均为
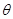，则下列判断正确的是：
