题目内容
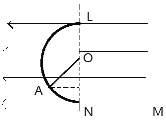
【题目】如图所示,在E=3×103V/m的水平向左匀强电场中,有一光滑半圆形绝缘轨道竖直放置,轨道与一水平绝缘轨道MN连接,半圆轨道所在竖直平面与电场线平行,其半径R=0.4 m,一带正电荷q=1×10-4 C的小滑块质量为m=0.04 kg,与水平轨道间的动摩擦因数μ=0.5,取g=10m/s2.要使小滑块恰能运动到半圆轨道的最高点L,求:
(1)滑块在水平轨道上释放时离N点的距离x
(2)滑块从释放到L点过程中的最大动能EKM

【答案】(1) 4m (2) 0.44J
【解析】
由题意可知考查与电场力有关圆周运动问题,根据牛顿第二定律、动能定理计算可得。
(1)滑块刚能通过轨道最高点的条件是
mg=m![]()
v=![]() =2m/s
=2m/s
滑块由释放点到最高点过程,由动能定理得:
qEx-μmgx-2mgR=![]() mv2
mv2
代入数据得:x=4m
(2)应用等效重力法分析,滑块受到重力电场力合力为恒力,与竖直方向夹角为37°时动能最大,从A点到最高点L过程中由动能定理:
-mg![]() R-qE
R-qE![]() R=
R=![]() mv2-EKM
mv2-EKM
得:EKM=0.44J

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目