题目内容
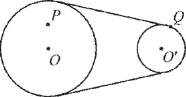
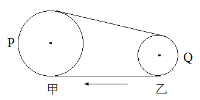
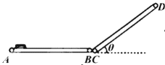
【题目】如图为仓库中常用的皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B两端相距3 m,另一台倾斜,传送带与地面的倾角θ=37°,C、D两端相距4.45 m,B、C相距很近。水平部分AB以5 m/s的速率顺时针转动。将质量为10 kg的一袋大米放在A端,到达B端后,速度大小不变地传到倾斜的CD部分,米袋与传送带间的动摩擦因数均为0.5。
(1)求米袋到达B端时的速度;
(2)若CD部分传送带不运转,求米袋沿传送带所能上升的最大距离;
(3)若要米袋能被送到D端,求CD部分顺时针运转的速度应满足的条件。
【答案】(1)5m/s(2)1.25m(3)vCD≥4m/s
【解析】
(1)米袋在AB上加速时的加速度:a0=μg=5m/s2
米袋的速度达到v0=5m/s时,滑行的距离:s0=![]() =2.5m<AB=3m,因此米袋在到达B点之前就有了与传送带相同的速度,即米袋到达B端时的速度5m/s;
=2.5m<AB=3m,因此米袋在到达B点之前就有了与传送带相同的速度,即米袋到达B端时的速度5m/s;
(2)设米袋在CD上运动的加速度大小为a,由牛顿第二定律得:mgsinθ+μmgcosθ=ma
代入数据得:a=10 m/s2
所以能滑上的最大距离:![]() =1.25m
=1.25m
(3)设CD部分运转速度为v1时米袋恰能到达D点(即米袋到达D点时速度恰好为零),则米袋速度减为v1之前的加速度为:a1=-g(sinθ+μcosθ)=-10 m/s2
米袋速度小于v1至减为零前的加速度为:
a2=-g(sinθ-μcosθ)=-2 m/s2
由![]()
解得:v1=4m/s,即要把米袋送到D点,CD部分的速度:vCD≥v1=4m/s

练习册系列答案
相关题目