题目内容
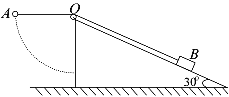
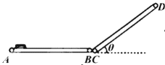
【题目】(多选)一根不可伸长的细线.上端悬挂在O点,下端系一个小球,如图(1)所示,某同学利用此装置来探究周期与摆长的关系.该同学用米尺测得细线两端的长度,用卡尺测量小球的直径,二者相加为l,通过改变细线的长度,测得对应的周期T,得到该装置的l-T2图像如图(2)所示.利用所学单摆相关知识,选择下列说法正确的选项(取π2=9.86)( )

A. T=2 s时摆长为1 m
B. T=2 s时摆长为0.994 m
C. 摆球半径为0.006 m
D. 当地重力加速度为9.80 m/s2
【答案】BCD
【解析】设摆长为l′,由单摆的周期公式T=2π![]() (l′=l-0.006m)并结合图2推导得:l=0.006+
(l′=l-0.006m)并结合图2推导得:l=0.006+![]() T2,可知
T2,可知![]() 为l-T2图象的斜率,所以有:
为l-T2图象的斜率,所以有:![]() =
=![]() ,解得:g=0.980m/s2,故D正确。由单摆的周期公式有:l′=
,解得:g=0.980m/s2,故D正确。由单摆的周期公式有:l′=![]() T2=
T2=![]() ×22=0.994m,故B正确,A错误;由图2可知,l-T2图象没有经过坐标原点,同时由l=0.006+
×22=0.994m,故B正确,A错误;由图2可知,l-T2图象没有经过坐标原点,同时由l=0.006+![]() T2可知,纵轴的截距为球的半径,故半径为r=0.006m,选项C正确,故选BCD。
T2可知,纵轴的截距为球的半径,故半径为r=0.006m,选项C正确,故选BCD。

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目