题目内容
【题目】如图所示，足够长的粗糙水平轨道AB上放置长木板m2和小滑块m3，小滑块m1置于m2的右端。m3与长木板m 2左端距离S=0.16m。现m1以水平向左的初速度v0=2.1m/s滑上长木板m 2的右端。当m 2与m 3发生弹性正碰（碰撞时间极短）后最终m 1和m 2均停下，且m 1还在长木板m 2上。己知m 1＝1.0kg，m 2=0.5kg，m 3=0.3kg，m 1与m 2之间动摩擦因数μ1=0.1、m 2与AB之间动摩擦因数μ2＝0.05、m 3与AB间摩擦不计，取g=10m/s2。求：
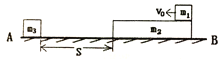
（1）m 2开始运动到与m 3发生碰撞经历的时间；
（2）m 2与m3碰撞结束瞬间，m 3的速度大小；
（3）m 2运动的总路程。
【答案】（1）0.8s（2）0.1m/s（3）0.65m
【解析】
(1)根据牛顿第二定律可知：小滑块
的加速度大小为
长木板
的加速度为
与
相撞时经过的时间t1，根据位移时间关系可得：
解得
此时小滑块的速度
长木板的速度
(2)与碰前的速度为
，长木板与小滑块发生弹性碰撞前后
由动量守恒：
由机械能守恒得：
解得：
；
(3)与相碰后，设、碰撞后经过时间
小滑块与长木板速度相同，设为v，则，
，
解得：
s；
恰好等于小滑块的速度，可知长木板不可能再与发生第二次碰撞。这段时间内长木板的位移
设此后长木板与小滑块一起以共同的加速度a做匀减速直线运动直到停止，因
所以
小于a；故成立，一起匀减速的位移
长木板运动的总路程
练习册系列答案
相关题目
