题目内容
13.如图所示,在竖直平面直角坐标系的第I、第Ⅳ象限中有垂直正交的匀强电场和匀强磁场,第I象限磁场方向垂直纸面向外,第Ⅳ象限磁场方向垂直纸面向里,大小都为B.电场方向竖直向上,且满足E=$\frac{mg}{q}$.现有质量为m、带电量为+q的带电小球从坐标原点以速度v沿y轴正方向射入,小球可视为质点.若在小球可能通过x轴的位置上依次放置小球1、小球2、小球3…(图中并未画出),它们的质量依次为m、2m、4m、…2n-1m,它们的带电量依次为+q、+2q、+4q…+2n-1q.设所有的碰撞时间极短,碰后都粘在一起且碰撞时电量不损失.求:
(1)小球第一次和第二次碰撞时的位置坐标
(2)小球最后趋近的位置坐标和整个运动过程中碰撞损失的总的机械能.
分析 (1)根据小球在磁场在洛伦兹力作用下做匀速圆周运动的半径公式,求得小球碰撞时的位置坐标,根据动量守恒求得小球碰撞后的速度,再根据半径公式求得第二次碰撞的位置坐标即可;
(2)根据小球碰撞过程中小球的电量表达式,再根据动量守恒求得粒子n次碰撞后的速度表达式再根据半径公式求得位置坐标的通项公式,再根据能量守恒求得损失的机械能.
解答 解:(1)在第I象限,因为$F=qE=q\frac{mg}{q}=mg$
所以带电小球在洛仑兹力的作用下做匀速圆周运动,由洛伦兹力提供向心力,有:
$qvB=m\frac{v^2}{R_0}$
得:${R_0}=\frac{mv}{qB}$…①
所以带电小球第一次碰撞时的位置坐标为:
($2\frac{mv}{qB}$,0)
小球第一次经过x轴时与小球1发生碰撞,由动量守恒定律得:
mv=2mv1
由题意知小球的带电量变为2q,在第IV象限满足2mg=2qE,小球在洛仑兹力作用下做小球匀速圆周运动有:
${R_1}=\frac{{2m{v_1}}}{2qB}=\frac{mv}{2qB}=\frac{1}{2}{R_0}$
所以带电小球第二次碰撞时的X坐标为:$2{R_0}+2{R_1}=3{R_0}=\frac{3mv}{qB}$
所以带电小球第二次碰撞时的位置坐标为($\frac{3mv}{qB}$,0)
(2)小球第n次经过x轴时与第n个小球发生碰撞后,设其质量为mn、电量为qn、速度为vn,则:
mn=m+m+2m+4m+…+2n-1m=2nm…②
${q_n}=q+q+2q+4q+…+{2^{n-1}}q={2^n}q$…③
因为${F_n}={q_n}E={2^n}q\frac{mg}{q}={2^n}mg$
所以每次碰后带电小球在洛仑兹力的作用下均做匀速圆周运动,由动量守恒定律得:mv=mnvn=P…④
又:${q_n}{v_n}B=m\frac{v_n^2}{R_n}$…⑤
由 ①②③④⑤式得:${R_n}=\frac{mv}{{{q_n}B}}=\frac{mv}{{{2^n}qB}}=\frac{1}{2^n}{R_0}$
当n→∞时,Rn→0,y轴的坐标y=0
当n→∞时,x轴的坐标为:
x=2R0+2R1+2R2+2R3…+2Rn=$2\frac{{{R_0}[1-{{(\frac{1}{2})}^n}]}}{{1-\frac{1}{2}}}=4{R_0}=\frac{4mv}{qB}$
所以小球趋近的坐标是$(\frac{4mv}{qB},0)$
当n→∞时,电场力、重力对小球都不做功
又当n→∞时,小球的质量mn→∞
所以,${E_{kn}}=\frac{P^2}{{2{m_n}}}→0$
即整个运动过程中因碰撞损失的最大总动能为:
$△{E_k}={E_{k0}}=\frac{1}{2}m{v^2}$
答:(1)小球第一次和第二次碰撞时的位置坐标分别为($2\frac{mv}{qB}$,0)和($\frac{3mv}{qB}$,0):
(2)小球最后趋近的位置坐标为$(\frac{4mv}{qB},0)$和整个运动过程中碰撞损失的总的机械能为$\frac{1}{2}m{v}^{2}$
点评 解决本题的关键是根据洛伦兹力提供圆周运动向心力,以及碰撞过程中的动量守恒,能根据题意写出电量及速度和半径的通项公式是正确解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
| A. | 2.62 s | B. | 2.40 s | C. | 2.20 s | D. | 2.00 s |
| A. | 若使放射性物质的温度升高,其半衰期将减小 | |
| B. | 发生α衰变时,生成核与原来的原子核相比,中子数减少了2个 | |
| C. | 太阳辐射的能量主要来自太阳内部的热核反应 | |
| D. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子动能减小,电势能增大,原子的总能量不变 | |
| E. | 贝克勒尔发现了天然放射现象,揭示了原子核内部有复杂结构 |
 如图所示,两个完全相同的圆弧轨道分别固定在竖直板上的不同高度处,轨道的末端水平,在它们相同位置上各安装一个电磁铁,两个电磁铁由同一个开关控制,通电后,两电磁铁分别吸住相同小铁球A、B,断开开关,两个小球同时开始运动.离开圆弧轨道后,A球做平抛运动,B球进入一光滑的水平轨道,则:
如图所示,两个完全相同的圆弧轨道分别固定在竖直板上的不同高度处,轨道的末端水平,在它们相同位置上各安装一个电磁铁,两个电磁铁由同一个开关控制,通电后,两电磁铁分别吸住相同小铁球A、B,断开开关,两个小球同时开始运动.离开圆弧轨道后,A球做平抛运动,B球进入一光滑的水平轨道,则: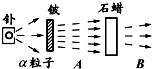 查德威克通过如图所示的实验装置,发现了中子,图中由天然放射性元素钋放出的α射线轰击铍49Be时产生粒子流A,用粒子流A轰击石蜡时,会打出粒子流B,则A为中子,B为质子,其核反应方程为49Be+24He→126C+10n.
查德威克通过如图所示的实验装置,发现了中子,图中由天然放射性元素钋放出的α射线轰击铍49Be时产生粒子流A,用粒子流A轰击石蜡时,会打出粒子流B,则A为中子,B为质子,其核反应方程为49Be+24He→126C+10n.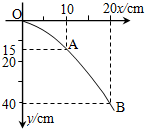 某学生在做“研究平抛运动”的实验中,忘记记下小球做平抛运动的起点位置,O为物体运动一段时间后的位置,取为坐标原点,平抛的轨迹如图示,根据轨迹的坐标求出物体做平抛运动的初速度为v0=1m/s,B点的速度为$\sqrt{10}$m/s,抛出点的坐标为(-10cm,-5cm).(g取10m/s2)
某学生在做“研究平抛运动”的实验中,忘记记下小球做平抛运动的起点位置,O为物体运动一段时间后的位置,取为坐标原点,平抛的轨迹如图示,根据轨迹的坐标求出物体做平抛运动的初速度为v0=1m/s,B点的速度为$\sqrt{10}$m/s,抛出点的坐标为(-10cm,-5cm).(g取10m/s2)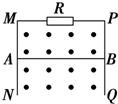 在竖直平面内有一平行光滑轨道MN、PQ,轨宽0.2m,在导轨间连接电阻R=0.2Ω,其他电阻不计,导轨间有一匀强磁场,B=0.5T,方向如图所示.有一导体棒AB质量m=0.01kg,能与导轨始终保持良好接触并能沿导轨滑动,AB从静止开始下滑,它能达到的最大速度是多少?(g取10m/s2)
在竖直平面内有一平行光滑轨道MN、PQ,轨宽0.2m,在导轨间连接电阻R=0.2Ω,其他电阻不计,导轨间有一匀强磁场,B=0.5T,方向如图所示.有一导体棒AB质量m=0.01kg,能与导轨始终保持良好接触并能沿导轨滑动,AB从静止开始下滑,它能达到的最大速度是多少?(g取10m/s2)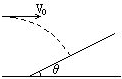 如图所示,以9.8m/s的水平速度V0抛出的物体,飞行一段时间后垂直地撞在倾角为θ=30°的斜面上 (g=9.8m/s2),求:
如图所示,以9.8m/s的水平速度V0抛出的物体,飞行一段时间后垂直地撞在倾角为θ=30°的斜面上 (g=9.8m/s2),求: