Question

【题目】如图，一块平板P2置于光滑水平面上，质量为2m ，其右端固定轻质弹簧，左端放置一个物体P1 ，质量为m可看作质点。平板P2上弹簧的自由端离物体P1相距为L的部分是粗糙的，其余部分是光滑，且P1与P2之间的动摩擦因数为μ 。现有一颗子弹P质量为以速度水平向右打入物体P1并留在其中，子弹打入过程时间极短。随后的运动过程中，（重力加速度为g）求

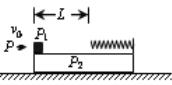
（1）子弹P打入物体P1后的共同速度v1

（2）若子弹P与物体P1最终能停在平板P2的最左端，则L至少为多少？

（3）试讨论动摩擦因数为μ与此过程中弹簧的最大弹性势能EP 的关系

Answer 1

【答案】 (1) （2）（3）若u>=时，Ep=0 若u<时，

【解析】

试题分析： （1）子弹P打入物体P1后的共同速度v1，根据动量守恒定律可得

，即

（2）到最后若子弹P与物体P1最终能停在平板P2的最左端，则最终所有物体的速度相同，由于在整个装置中，系统总合外力为零，设最终速度为，则

求得

（3）若u>=时，则可能在为碰到弹簧前就已经与P2达到共同速度，即Ep=0

若u<时，则当两者速度相等时，弹簧弹性势能最大，根据可知达到共同速度为，弹性势能为