题目内容
【题目】如图所示，光滑水平面AB与竖直面内的半圆形导轨在B点相切，半圆形导轨的半径为R一个质量为m的物体将弹簧压缩至A点后由静止释放，在弹力作用下物体获得某一向右的速度后脱离弹簧，当它经过B点进入导轨的瞬间对轨道的压力为其重力的8倍，之后向上运动恰能到达最高点C （不计空气阻力）试求：
（1）物体在A点时弹簧的弹性势能；
（2）物体从B点运动至C点的过程中阻力所做的功；
（3）物体离开C点后落回水平面时的位置与B点的距离。
【答案】（1）3.5mgR（2）－mgR（3）2R
【解析】(1)设物体在B点的速度为vB，对轨道的压力为FNB，
则有：FNB－mg＝
又FNB＝8mg ∴
mvB2＝3.5mgR
由能量转化与守恒定律可知：弹性势能Ep＝
mvB2＝3.5mgR……………….(4分)
(2)设物体在C点的速度为vC
由题意可知：mg＝
物体从B点运动到C点的过程中，设阻力做的功为W，由动能定理得W－2mgR＝
mvC2－
mvB2
解得W＝－mgR………………………(4分)
(3)物体离开C点后做平抛运动，设落地点与B点的距离为s，
由平抛运动规律得s＝vCt,2R＝
gt2
解得s＝2R………………………. （2分）
本题考查圆周运动，在B点由弹力和重力提供向心力，由A点到B点，弹簧的弹性势能转化为物体的动能，由此可求得弹性势能，在C点由重力提供向心力，从B点到C点应用动能定理可求得克服阻力做功
【题型】解答题
【结束】
12
【题目】一平台的局部如图甲所示，水平面光滑，竖直面粗糙，物体B与竖直面动摩擦因数μ=0.5，右角上固定一定滑轮，在水平面上放着一质量mA=1.0kg，大小可忽略的物块A，一轻绳绕过定滑轮，轻绳左端系在物块A上，右端系住物块B，物块B质量mB=1.0kg物块B刚好可与竖直面接触。起始时令两物体都处于静止状态，绳被拉直，设物体A距滑轮足够远，台面足够高，最大静摩擦力等于滑动摩擦力，忽略滑轮质量及其与轴之间的摩擦，g取10m/s2，求
（1）同时由静止释放AB，经t=1s，则A的速度多大；
（2）同时由静止释放AB，同时也对物块B施加力F，方向水平向左，大小随时间变化如图乙所示，求物块B运动过程中的最大速度和物块B经多长时停止运动。
【答案】见解析。
【解析】试题分析：依题得:（1）对AB为系统:
（2）AB先做加速度减少的加速运动,在AB加速度减为零之前,AB一起运动,绳子拉紧．
（k=20N/s）
AB为系统:
得:
画a-t图如右:0-1s, a=0,
,速度最大为三角形面积:
当在B开始减速时,绳子松弛,A匀速,B减速
对B:
得:
（t≥1s）如图
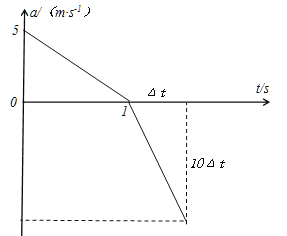
速度要为零,总面积为零,即两三角形面积相等．得: 
