题目内容
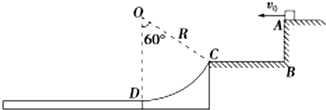
(16分)如图所示,倾角为37°的粗糙斜面AB底端与半径R=0.4m的光滑半圆轨道BC平滑相连,O为轨道圆心,BC为圆轨道直径且处于竖直方向,A、C两点等高,质量m=1kg的滑块从A点由静止开始下滑,恰能滑到与O等高的D点,g取10m/s2,sin37°=0.6,cos37°=0.8。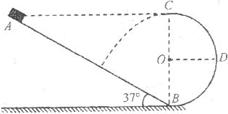
⑴求滑块与斜面间的动摩擦因数μ;
⑵若使滑块能到达C点,求滑块从A点沿斜面滑下时的初速度v0的最小值;
⑶若滑块离开C处的速度大小为4m/s,求滑块从C点飞出至落到斜面上的时间t。
⑴μ=0.375;⑵v0min=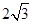 m/s;⑶t=0.2s
m/s;⑶t=0.2s
解析试题分析:⑴滑块在整个运动过程中,受重力mg、接触面的弹力N和斜面的摩擦力f作用,弹力始终不做功,因此在滑块由A运动至D的过程中,根据动能定理有:mgR-μmgcos37°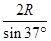 =0-0
=0-0
解得:μ=0.375
⑵滑块要能通过最高点C,则在C点所受圆轨道的弹力N需满足:N≥0 ①
在C点时,根据牛顿第二定律有:mg+N=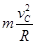 ②
②
在滑块由A运动至C的过程中,根据动能定理有:-μmgcos37°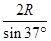 =
=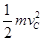 -
- ③
③
由①②③式联立解得滑块从A点沿斜面滑下时的初速度v0需满足:v0≥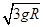 =
=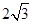 m/s
m/s
即v0的最小值为:v0min=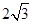 m/s
m/s
⑶滑块从C点离开后将做平抛运动,根据平抛运动规律可知,在水平方向上的位移为:x=vt ④
在竖直方向的位移为:y=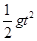 ⑤
⑤
根据图中几何关系有:tan37°=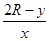 ⑥
⑥
由④⑤⑥式联立解得:t=0.2s
考点:本题主要考查了牛顿第二定律、平抛运动规律、动能定理的应用问题,属于中档题。

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目


 如图所示,在光滑水平地面上有一固定的挡板,挡板左端固定一个轻弹簧。现有一质量M=3kg,长L=4m的小车AB(其中
如图所示,在光滑水平地面上有一固定的挡板,挡板左端固定一个轻弹簧。现有一质量M=3kg,长L=4m的小车AB(其中 为小车的中点,
为小车的中点, 部分粗糙,
部分粗糙, 部分光滑)一质量为m=1kg的小物块(可视为质点),放在车的最左端,车和小物块一起以
部分光滑)一质量为m=1kg的小物块(可视为质点),放在车的最左端,车和小物块一起以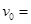 4m/s的速度在水平面上向右匀速运动,车撞到挡板后瞬间速度变为零,但未与挡板粘连。已知车
4m/s的速度在水平面上向右匀速运动,车撞到挡板后瞬间速度变为零,但未与挡板粘连。已知车 0.3,重力加速度
0.3,重力加速度 。求:
。求:
 端多远。
端多远。 )。求:
)。求:
 的光滑1/4圆形轨道,BC段为高为h=5
的光滑1/4圆形轨道,BC段为高为h=5 的小球由A点从静止开始下滑到B点时速度的大小为2
的小球由A点从静止开始下滑到B点时速度的大小为2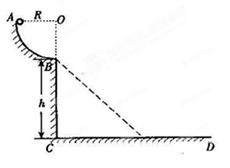
 =45°的斜面(如图中虚线所示),那么小球离开B点后能否落到斜面上?如果能,求它第一次落在斜面上的位置。
=45°的斜面(如图中虚线所示),那么小球离开B点后能否落到斜面上?如果能,求它第一次落在斜面上的位置。