题目内容
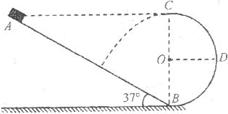
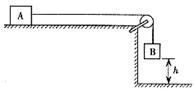
(12分)如图所示,水平绝缘轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接,半圆形轨道的半径R=0.40m。轨道所在空间存在水平向右的匀强电场,电场强度E=1.0×104 N/C。现有一电荷量q=+1.0×10-4C,质量m="0.10" kg的带电体(可视为质点),在水平轨道上的P点由静止释放,带电体运动到圆形轨道最低点B时的速度vB=5.0m/s。已知带电体与水平轨道间的动摩擦因数μ=0.50,重力加速度g=10m/s2。求:
(1)带电体运动到圆形轨道的最低点B时,圆形轨道对带电体支持力的大小;
(2)带电体在水平轨道上的释放点P到B点的距离L1;
(3)带电体第一次经过C点后,落在水平轨道上的位置到B点的距离L2。
(1)7.25N;(2)2.5m;(3)0.4m;
解析试题分析:(1)在最低点时,根据牛顿第二定律和圆周运动公式有: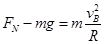 (2分)
(2分)
代入数据解得: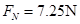 (1分)
(1分)
(2)从P点到B点由动能定理得: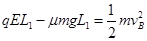 (2分)
(2分)
代入数据解得: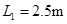 (1分)
(1分)
(3)物体从B点到达C点,由动能定理得: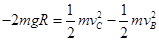 (2分)
(2分)
第一次经过C点后,水平方向作匀减速直线运动,竖直方向做自由落体运动,故有: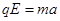 (1分)
(1分)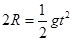 (1分)
(1分)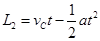 (1分)
(1分)
联立解得: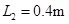 (1分)
(1分)
考点:运动的合成分解、动能定理、圆周运动、静电场、牛顿第二定律

练习册系列答案
相关题目
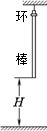
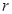 为0.2m,在圆心O处固定一个电荷量为-
为0.2m,在圆心O处固定一个电荷量为-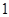 .0×
.0×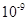 C的点电荷。质量为0.06kg、略小于圆管截面的带电小球,从与O点等高的A点沿圆管内由静止运动到最低点B ,到达B点小球刚好与圆弧没有作用力,然后从B点进入板距d= 0.08m的两平行板电容器后刚好能在水平方向上做匀速直线运动,且此时电路中的电动机刚好能正常工作。已知电源的电动势为12V,内阻为1Ω,定值电阻R的阻值为6Ω,电动机的内阻为0.5Ω.求(取g=10m/s2,静电力常量k="9.0" ×109 N·m2/C2)
C的点电荷。质量为0.06kg、略小于圆管截面的带电小球,从与O点等高的A点沿圆管内由静止运动到最低点B ,到达B点小球刚好与圆弧没有作用力,然后从B点进入板距d= 0.08m的两平行板电容器后刚好能在水平方向上做匀速直线运动,且此时电路中的电动机刚好能正常工作。已知电源的电动势为12V,内阻为1Ω,定值电阻R的阻值为6Ω,电动机的内阻为0.5Ω.求(取g=10m/s2,静电力常量k="9.0" ×109 N·m2/C2)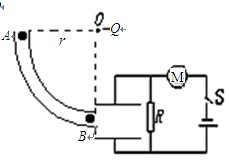
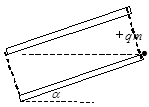
 角的绝缘直杆
角的绝缘直杆 ,其下端(
,其下端( 端)距地面高度
端)距地面高度 。有一质量
。有一质量 的带电小环套在直杆上,正以某一速度,沿杆匀速下滑,小环离杆后正好通过
的带电小环套在直杆上,正以某一速度,沿杆匀速下滑,小环离杆后正好通过 点处。(
点处。( 取
取
 ,
, )
)