题目内容

8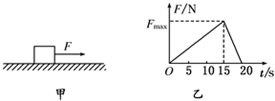．如图甲所示，用水平向右的力F拉放在光滑水平地面上、质量为500kg的物体，作用时间为20s，使物体获得0.5m/s的速度．若力F大小的变化为：前15s从零开始随时间均匀增大，后5s均匀减小为零，如图乙所示，求：
（1）力F对物体的冲量；
（2）力F的平均值．

分析 （1）根据动量定理求解拉力的冲量；
（2）F-t图象与时间轴包围的面积表示拉力的冲量．

解答 解：（1）拉力对物体的冲量等于物体的动量增加，有：
IF=mv=500×0.5N•s=250N•s
（2）由于拉力均匀变化，设拉力的平均值为F，则拉力的冲量大小为图乙中图线与时间轴线所围成的面积，则：
IF=F•t
得：F=12.5N．
答：（1）力F对物体的冲量为250N•s；
（2）力F的最大值为12.5N

点评 本题关键是根据动量定理列式求解，注意F-t图象中图线与t轴包围的面积表示拉力F的冲量大小，不难．

练习册系列答案
相关题目
18．在光滑水平地面上有一凹槽A，中央放一小物块B，物块与左右两边槽壁的距离如图所示，L为2.0m，凹槽与物块的质量均为m，两者之间的动摩擦因数μ为0.05，开始时物块静止，凹槽以v0=5m/s初速度向右运动，设物块与凹槽槽壁碰撞过程中没有能量损失，且碰撞时间不计．g取10m/s2．
求：（1）物块与凹槽相对静止时的共同速度；
（2）从凹槽开始运动到两者相对静止物块与左、右侧槽壁碰撞的总次数；物块B最终停在何处？
（3）从凹槽开始运动到两者刚相对静止所经历的时间及该时间内凹槽运动的位移大小．
19．已知金刚石的密度为ρ=3.5×103kg/m3，摩尔质量为12×10-3kg/m3，现有一块体积为4.0×10-8m3的一小块金刚石，它含有多少个碳原子？（保留两位有效数字）假如金刚石中的碳原子是紧密地挨在一起，试估算碳原子的直径．（保留一位有效数字）
16．物体沿直线运动的v-t关系如图所示，已知在第1s内合外力对物体做的功为W，则（　　）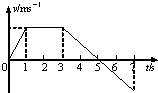
A．从第1s末到第3s末合外力做功为0
B．从第3s末到第5s末合外力做功为-W
C．从第5s末到第7s末合外力做功为-W
D．从第3s末到第4s末合外力做功为-0.75W
3．欲用伏安法测定一段阻值约为5Ω左右的金属导线的电阻，要求测量结果尽量准确，现备有以下器材：
A．电源（3V，内阻不计）
B．电流表（0～3A，内阻约0.0125Ω）
C．电流表（0～0.6A，内阻约0.125Ω）
D．电压表（0～3V，内阻约3kΩ）
E．电压表（0～15V，内阻约15kΩ）
F．滑动变阻器（0～20Ω，额定电流1A）
G．滑动变阻器（0～2 000Ω，额定电流0.3A）
H．开关、导线
（1）上述器材中应选用的是ACDFH；（填写各器材的字母代号）
（2）设实验中，电流表、电压表的某组示数如图所示，图示中I=0.48A，U=2.20V．

（3）为使通过待测金属导线的电流能在0～0.5A范围内改变，请按要求画出测量待测金属导线的电阻Rx的原理电路图．
13．关于重力势能与重力做功，下列说法中正确的是（　　）
A．重力做的功等于重力势能的增加
B．在同一高度，将物体以初速v0向不同的方向抛出，从抛出到落地过程中，重力做的功相等，物体所减少的重力势能一定相等
C．重力势能等于零的物体，不可能对别的物体做功
D．用手托住一个物体匀速上举时，手的支持力做的功等于克服重力的功与物体所增加的重力势能之和
20．阿伏加德罗常数为NA，铜的摩尔质量为M，铜的密度为ρ，则下列说法正确的是（　　）
A．1kg铜所含原子数为ρNAB．1m3铜所含原子数为$\frac{ρ{N}_{A}}{M}$
C．1个铜原子的质量为$\frac{M}{{N}_{A}}$D．1个铜原子所占的体积为$\frac{M}{ρ{N}_{A}}$
17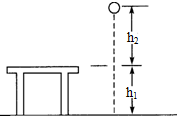．如图所示，桌面高为h1，质量为m的小球从高出桌面h2的A点下落到地面上的B点，在此过程中小球的重力势能（　　）
A．增加mgh2B．增加mg（h1+h2）C．减少mgh2D．减少mg（h1+h2）
20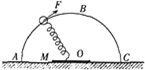．如图所示，一粗糙程度处处相同的竖直半圆形框架ABC固定在水平面上，框架下面放一块厚度忽略不计的金属板，金属板的中心O点位于框架的圆心处，框架上套有一个重力不计的轻圆环，用轻弹簧把圆环与金属板的O点连接，开始轻弹簧处于水平拉紧状态．用一个始终沿框架切线方向的拉力F拉动圆环从左侧水平位置缓慢绕框架运动，直到轻弹簧达到竖直位置，金属板始终保持静止状态，则在整个过程中（　　）
A．水平面对金属板的支持力逐渐减小B．水平面对金属板的摩擦力逐渐增大
C．拉力F大小不变D．框架对圆环的摩擦力逐渐增大

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网