题目内容
18. 在光滑水平地面上有一凹槽A,中央放一小物块B,物块与左右两边槽壁的距离如图所示,L为2.0m,凹槽与物块的质量均为m,两者之间的动摩擦因数μ为0.05,开始时物块静止,凹槽以v0=5m/s初速度向右运动,设物块与凹槽槽壁碰撞过程中没有能量损失,且碰撞时间不计.g取10m/s2.
在光滑水平地面上有一凹槽A,中央放一小物块B,物块与左右两边槽壁的距离如图所示,L为2.0m,凹槽与物块的质量均为m,两者之间的动摩擦因数μ为0.05,开始时物块静止,凹槽以v0=5m/s初速度向右运动,设物块与凹槽槽壁碰撞过程中没有能量损失,且碰撞时间不计.g取10m/s2.求:(1)物块与凹槽相对静止时的共同速度;
(2)从凹槽开始运动到两者相对静止物块与左、右侧槽壁碰撞的总次数;物块B最终停在何处?
(3)从凹槽开始运动到两者刚相对静止所经历的时间及该时间内凹槽运动的位移大小.
分析 (1)碰撞过程中动量守恒,根据动量守恒定律列式即可求解速度;
(2)对整体根据动能定理求出A、B相对静止时,A、B间的相对路程,然后求出碰撞次数与B的位置;
(3)设凹槽与物块碰前的速度分别为v1、v2,碰后的速度分别为v1′、v2′.根据动量守恒定律及能量守恒定律列式可知,每碰撞一次凹槽与物块发生一次速度交换,在同一坐标系上两者的速度图线,根据碰撞次数可分为13段,凹槽、物块的v-t图象在两条连续的匀变速运动图线间转换,故可用匀变速直线运动规律求时间,凹槽的v-t图象所包围的阴影面积即为凹槽的位移大小.
解答 解:(1)设两者间相对静止时的速度为v,设向右为正方向,
则由动量守恒定律得:mv0=2mv, 解得:v=2.5m/s;
解得:v=2.5m/s;
(2)物块与凹槽间的滑动摩擦力f=μN=μmg,
设两者间相对静止前,相对运动的路程为s1,
由动能定理得:-fs1=$\frac{1}{2}$•2mv2-$\frac{1}{2}$mv02,
解得:s1=12.5m,
已知L=2m,物块与左、右侧槽壁碰撞的总次数是6次,
物块B最终停在距左侧槽臂的距离为:12.5-1-2×5=1.5m处.
(2)设凹槽与物块碰前的速度分别为v1、v2,碰后的速度分别为v1′、v2′.
以槽的初速度方向为正方向,由动量守恒定律得:mv1+mv2=mv1′+mv2′,
由机械能守恒定律得:$\frac{1}{2}$mv12+$\frac{1}{2}$mv22=$\frac{1}{2}$mv1′2+$\frac{1}{2}$mv2′2,
解得:v1′=v2,v2′=v1,即每碰撞一次凹槽与物块发生一次速度交换,在同一坐标系上两者的速度图线如图所示,
根据碰撞次数可分为13段,凹槽、物块的v-t图象在两条连续的匀变速运动图线间转换,
故可用匀变速直线运动规律求时间.则
v=v0+at,a=-μg,
解得:t=5s
凹槽的v-t图象所包围的阴影面积即为凹槽的位移大小s2.(等腰三角形面积共分13份,第一份面积为0.5L.其余每份面积均为L.)
s2=$\frac{1}{2}$$\frac{{v}_{0}}{2}$t+6.5L=$\frac{1}{2}$×$\frac{5}{2}$×5+6.5×2=19.25m;
答:(1)物块与凹槽相对静止时的共同速度为2.5m/s;
(2)从凹槽开始运动到两者相对静止物块与左、右侧槽壁碰撞的总次数为6次;物块B最终停在距左侧槽臂的距离为1.5m处.
(3)从凹槽开始运动到两者刚相对静止所经历的时间为5s,该时间内凹槽运动的位移大小为19.25m.
点评 本题主要考查了动量守恒定律、动能定理及能量守恒定律的直接应用,要求同学们能正确分析物体的运动情况,能根据题意画出速度-时间图象,难度适中.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案| A. |  | B. |  | C. |  | D. |  |
 质量和电量都相等的带电粒子M和N,以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,下列表述不正确的是( )
质量和电量都相等的带电粒子M和N,以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,下列表述不正确的是( )| A. | M带负电,N带正电 | B. | 洛伦磁力对M做负功、对N做正功 | ||
| C. | M的运行时间等于N的运行时间 | D. | M的速度率大于N的速率 |
| A. | 因为功有正功和负功的区别,所以功是矢量 | |
| B. | 若物体的速度在变化,则动能也一定在变化 | |
| C. | 重力势能减少,重力一定对物体做正功 | |
| D. | 一个物体在平衡力的作用下运动,机械能一定不变 |
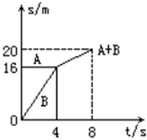 如图所示,A、B两物体的质量分别为3kg与1kg,相互作用后沿同一直线运动,它们的位移-时间图象如图所示,则A物体在相互作用前后的动量变化是3kg?m/s,B物体在相互作用前后的动量变化是-3kg?m/s,相互作用前后A、B系统的总动量不变.(填“变大”“变小”或“不变”)
如图所示,A、B两物体的质量分别为3kg与1kg,相互作用后沿同一直线运动,它们的位移-时间图象如图所示,则A物体在相互作用前后的动量变化是3kg?m/s,B物体在相互作用前后的动量变化是-3kg?m/s,相互作用前后A、B系统的总动量不变.(填“变大”“变小”或“不变”)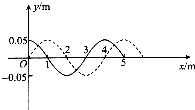 如图所示,实线为简谐波在t时刻的图线,虚线为波在(t+0.01)s时刻的图线
如图所示,实线为简谐波在t时刻的图线,虚线为波在(t+0.01)s时刻的图线 如图甲所示,用水平向右的力F拉放在光滑水平地面上、质量为500kg的物体,作用时间为20s,使物体获得0.5m/s的速度.若力F大小的变化为:前15s从零开始随时间均匀增大,后5s均匀减小为零,如图乙所示,求:
如图甲所示,用水平向右的力F拉放在光滑水平地面上、质量为500kg的物体,作用时间为20s,使物体获得0.5m/s的速度.若力F大小的变化为:前15s从零开始随时间均匀增大,后5s均匀减小为零,如图乙所示,求: