题目内容
如图所示,某货物仓库,需将生产成品用传送带从底端传递到高度为H的高处存放,货物从静止开始轻放到传送带的最下端,已知货物与传送带间的动摩擦因数为μ= ,传送带始终保持恒定速度运动。若想用最短时间将货物匀加速的运送至顶端,则传送带与水平面夹角θ应设计为多大?最短时间为多少?(传送带长度可随设计需要而变化,g=10m/s2)
,传送带始终保持恒定速度运动。若想用最短时间将货物匀加速的运送至顶端,则传送带与水平面夹角θ应设计为多大?最短时间为多少?(传送带长度可随设计需要而变化,g=10m/s2)
 ,传送带始终保持恒定速度运动。若想用最短时间将货物匀加速的运送至顶端,则传送带与水平面夹角θ应设计为多大?最短时间为多少?(传送带长度可随设计需要而变化,g=10m/s2)
,传送带始终保持恒定速度运动。若想用最短时间将货物匀加速的运送至顶端,则传送带与水平面夹角θ应设计为多大?最短时间为多少?(传送带长度可随设计需要而变化,g=10m/s2)
当 =30
=30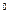 时,货物运动最短时间为t=2
时,货物运动最短时间为t=2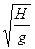
 =30
=30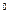 时,货物运动最短时间为t=2
时,货物运动最短时间为t=2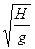
对物体受力分析如图所示,物体向上运动的加速度为:a= gcos
gcos —gsin
—gsin …….3分
…….3分
物体做匀加速运动则:

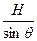 =
=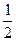 (
( gcos
gcos —gsin
—gsin )t
)t …………….3分
…………….3分
物体上升运动的时间:t=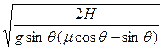 …4分
…4分
而sin (
( cos
cos —sin
—sin )=
)=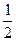
 sin2
sin2 —
—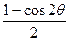 =
=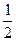 (
(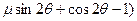 )
)
又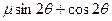 =
=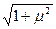 sin(2
sin(2 +
+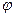 )
)
因sin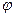 =
=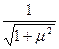 所以
所以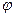 =30
=30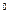
故当 =30
=30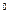 时,
时,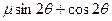 取最大值为2………………………………3分
取最大值为2………………………………3分
所以,当 =30
=30 时,货物运动最短时间为t=2
时,货物运动最短时间为t=2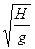 ……………………………...3分
……………………………...3分
 gcos
gcos —gsin
—gsin …….3分
…….3分物体做匀加速运动则:

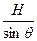 =
=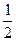 (
( gcos
gcos —gsin
—gsin )t
)t …………….3分
…………….3分物体上升运动的时间:t=
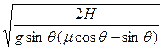 …4分
…4分而sin
 (
( cos
cos —sin
—sin )=
)=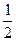
 sin2
sin2 —
—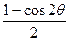 =
=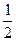 (
(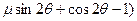 )
)又
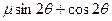 =
=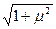 sin(2
sin(2 +
+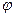 )
)因sin
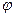 =
=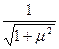 所以
所以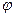 =30
=30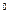
故当
 =30
=30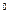 时,
时,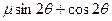 取最大值为2………………………………3分
取最大值为2………………………………3分所以,当
 =30
=30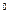 时,货物运动最短时间为t=2
时,货物运动最短时间为t=2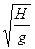 ……………………………...3分
……………………………...3分
练习册系列答案
相关题目

 的加速度匀减速下降,到达地面时速度为4m/s.(g取10m/
的加速度匀减速下降,到达地面时速度为4m/s.(g取10m/ 竖直上抛一物体
竖直上抛一物体 ,相隔
,相隔 时间后又以初速度
时间后又以初速度 从地面上竖直上抛另一物体
从地面上竖直上抛另一物体 ,要使
,要使





