题目内容
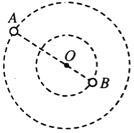
【题目】宇航员乘坐宇宙飞船来到某行星附近，关闭发动机让飞船绕星球做半径为r的匀速圆周运动，周期为T．已知万有引力常量为G，忽略其他天体对飞船的影响，
（1） 试求该行星的质量；
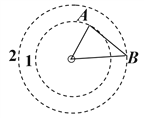
（2）将行星用右图的圆1表示，用圆2表示飞船运动轨迹，宇航员发现该行星的视角为2α，α即图中的∠ABO，试估计在该星球表面发射该星球的卫星所需要获得的最小发射速度；
（3）如果宇航员操纵发动机使飞船在B点进行了一次恰当的瞬间减速，然后关闭发动机，使飞船绕该行星做椭圆轨 道运动，且椭圆轨道的离行星最近处到行星表面距离可以忽略，求飞船在此椭圆轨道上运行的周期．
【答案】（1）
;（2） 
;（3）
【解析】（1）由
得： 
（2）由几何关系可以知道该行星的半径为： 
由万有引力公式知： 
得发射的最小速度为：
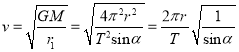
（3）飞船做椭圆运动的半长轴为
由开普勒第三定律知：
解得： 
综上所述本题答案是：（1）
，（2）
（3）
练习册系列答案
科学实验活动册系列答案
相关题目
