题目内容
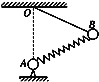
【题目】某砂场为提高运输效率,研究砂粒下滑的高度与砂粒在传送带上运动的关系,建立如图所示的物理模型。竖直平面内有一倾角θ=37°的直轨道AB,其下方右侧放置一水平传送带,直轨道末端B与传送带间距可近似为零,但允许砂粒通过。转轮半径R=0.4m、转轴间距L=2m的传送带以恒定的线速度逆时针转动,转轮最低点离地面的高度H=2.2m。现将一小物块放在距离传送带高h处静止释放,假设小物块从直轨道B端运动到达传送带上C点时,速度大小不变,方向变为水平向右。已知小物块与直轨道和传送带间的动摩擦因数均为μ=0.5。(sin37°=0.6;g=10m/s2)
(1)若h=2.4m,求小物块到达B端时速度的大小;
(2)改变小物块释放的高度h,小物块从传送带的D点水平向右抛出,求小物块落地点到D点的水平距离x与h的关系式及h需要满足的条件。

【答案】(1)![]() ;(2)
;(2)![]() h≥3.6m
h≥3.6m
【解析】
(1)物块由A到B的过程中,由牛顿第二定律可得:
![]()
由运动学公式可得:
![]()
联立,代入数据可解得:
![]()
(2)从A到D的过程中,由动能定理可得:
![]()
从D点抛出后,由平抛运动规律可得:
![]()
![]()
联式可解得:
![]()
为使能在D点水平抛出则满足条件为:
![]()
代入数据可解得:
![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】因测试需要,一辆汽车在某雷达测速区,沿平直路面从静止开始匀加速一段时间后,接着做匀减速运动直到最后停止.下表中给出了雷达测出的部分时刻对应的汽车速度数值.
时刻/s | 0 | 1.0 | 2.0 | … | 7.0 | 8.0 | 9.0 |
速度/ms﹣1 | 0 | 4.0 | 8.0 | … | 4.0 | 2.0 | 0 |
求:(1)汽车匀加速和匀减速两阶段的加速度a1、a2分别是多少?
(2)汽车运动过程中的最大速度;
(3)前5秒内汽车的位移.