题目内容
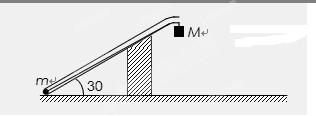
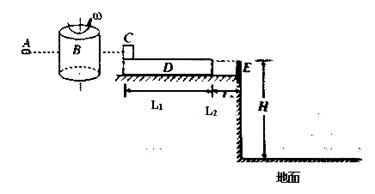
（18分）如图所示，质量为m1=0.01Kg的子弹A，垂直纸筒的旋转轴穿过高速旋转的纸筒B且只在B上留下一个弹孔，子弹穿过B后打入质量为m2=0.99Kg的木块C中，并在C里面（A、C可视为质点）。木块C放在长木板D的左端，D的质量m3=3kg，长度为L1=0.375m。长木板刚在光滑的水平桌面上，水平桌面的右端有一很薄的与D等高的固定挡板E，D的右端到E距离L2=0.125m，D碰到即被粘牢，C则离开D飞到桌面下方的水平地面上。已知纸筒直径d=30cm，纸筒匀速旋转的角速度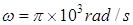
，C与D之间的动摩擦因素
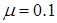，木板D的上表面距离地面高H=5m，子弹穿过纸筒的过程中所受的摩擦力和空气阻力忽略不计，取g=10m/s2。求：
（1）若发生子弹的枪有两个档位，可以发射两种初速度不同的子弹，为了让子弹穿过纸筒的时间尽可能短，子弹两个档位的速度大小分别是多少？
（2）在（1）问中，讨论子弹打入C后，整体能否与D达到共同速度，并求出AC整体能与D达到共速情况下AC整体落到地面上距桌边的距离。
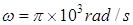，C与D之间的动摩擦因素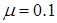，木板D的上表面距离地面高H=5m，子弹穿过纸筒的过程中所受的摩擦力和空气阻力忽略不计，取g=10m/s2。求：（1）若发生子弹的枪有两个档位，可以发射两种初速度不同的子弹，为了让子弹穿过纸筒的时间尽可能短，子弹两个档位的速度大小分别是多少？
（2）在（1）问中，讨论子弹打入C后，整体能否与D达到共同速度，并求出AC整体能与D达到共速情况下AC整体落到地面上距桌边的距离。
（1）300m/s ；100m/s（2）0.25m。
试题分析：（1）依题意，枪由两个档位，且穿过纸筒后只留下一个弹孔，要增大穿过纸筒的时间尽可能的短，纸筒转过的角度应满足：α=（2n+1）π，式中n取0和1
子弹穿过纸筒的时间为：
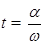
则子弹的速度为：
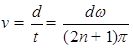…①把n=0，1分别代入①式得子弹的速度分别为：
v1=300m/s v2=100m/s
（2）设子弹击中木块C并留住其中的共同速度为v11，由动量守恒定律得：
m1v=（m1+m2）v11…②
假设AC能够与D到达共同的速度v22，由动量守恒定律得：
（m1+m2）v11=（m1+m2+m3）v22… ③
设此过程中AC相对于D滑动的位移是s1，由能量守恒定律得：
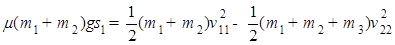… ④联立②③④得：
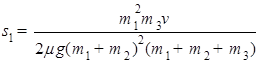…⑤讨论：Ⅰ当v=v1=300m/s时，代入⑤式得：s1=3.375m＞L1
说明此种情况下AC与D不能共速．
Ⅱ当v=v2=100m/s时，代入⑤式解得：s2=0.375m=L2
说明此种情况下AC刚好没有滑离D．
设此过程中D对桌面的位移是S 2，由动能定理得：
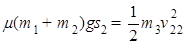…⑥联立②③⑥式．并代入数据解得：
s2=0.09375m＜0.125m=L2… ⑦
由⑦式知，AC整体刚好滑到D的右端时，还没有与E碰撞，说明此种情况下AC能与D共速，
当D与E碰撞并粘牢后，AC整体做平抛运动，设落到水平地面上的距离为s，由运动学的知识：
平抛运动的时间：
位移：s=v22?t=0.25×1m=0.25m
练习册系列答案
相关题目
，减少的动能有
转化成电势能，那么，当它再次经过B点时动能为（ ）
处。为了确保运动员的安全，试计算：
，a、b分别为长半轴和短半轴）
) 
