题目内容
(14分)如图所示,长为l、内壁光滑的直管与水平地面成30°角固定放置,上端管口水平,且水平部分管口长度忽略不计,质量为m的小球可在直管内自由滑动,用一根轻质光滑细线将小球与另一质量为M的物块相连,M=3m。开始时小球固定于管底,物块悬挂于管口,小球、物块均可视为质点。将小球释放,小球在管口的转向过程中速率不变。试求:
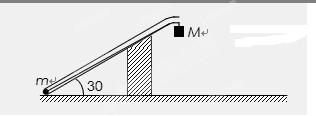
(1)物块落地前瞬间的速度大小;
(2)小球做平抛运动的水平位移;(M落地后绳子一直松弛)
(3)有同学认为,若取M=km,则k足够大时,能使小球平抛运动水平位移的大小最大达到绳长l,请通过计算判断这种说法是否正确。

(1)物块落地前瞬间的速度大小;
(2)小球做平抛运动的水平位移;(M落地后绳子一直松弛)
(3)有同学认为,若取M=km,则k足够大时,能使小球平抛运动水平位移的大小最大达到绳长l,请通过计算判断这种说法是否正确。
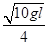
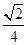 l 错误
l 错误 (1)系统机械能守恒
Mgl sin30°=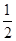 (m+M) v12+mgsin30°l sin30° ① (2分)
(m+M) v12+mgsin30°l sin30° ① (2分)
因为M=3m,得v1=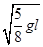 =
=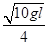 (1分)
(1分)
(2)根据动能定理
-mgsin30°(l -l sin30°) =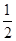 mv22-
mv22-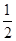 mv12 ② (2分)
mv12 ② (2分)
m飞出管口时的速度v2=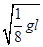 (1分)
(1分)
m在空中飞行的时间t=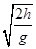 =
= 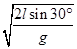 =
=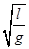 (1分)
(1分)
水平位移S=v2 t=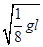
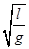 =
=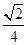 l (1分)
l (1分)
(3)若M=km,由①②两式可得
m飞出管口时的速度v2=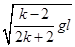 (2分)
(2分)
水平位移S=v2 t=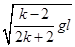
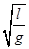 =
=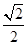
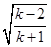 l (2分)
l (2分)
可以得出结论,S <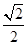 l (1分)
l (1分)
所以,这种说法是 的,水平位移不可能为l。 (1分)
Mgl sin30°=
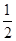 (m+M) v12+mgsin30°l sin30° ① (2分)
(m+M) v12+mgsin30°l sin30° ① (2分)因为M=3m,得v1=
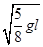 =
=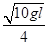 (1分)
(1分)(2)根据动能定理
-mgsin30°(l -l sin30°) =
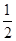 mv22-
mv22-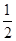 mv12 ② (2分)
mv12 ② (2分)m飞出管口时的速度v2=
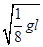 (1分)
(1分)m在空中飞行的时间t=
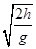 =
= 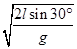 =
=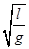 (1分)
(1分)水平位移S=v2 t=
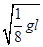
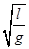 =
=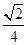 l (1分)
l (1分)(3)若M=km,由①②两式可得
m飞出管口时的速度v2=
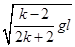 (2分)
(2分)水平位移S=v2 t=
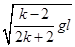
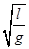 =
=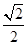
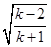 l (2分)
l (2分)可以得出结论,S <
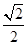 l (1分)
l (1分)所以,这种说法是 的,水平位移不可能为l。 (1分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,C与D之间的动摩擦因素
,C与D之间的动摩擦因素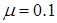 ,木板D的上表面距离地面高H=5m,子弹穿过纸筒的过程中所受的摩擦力和空气阻力忽略不计,取g=10m/s2。求:
,木板D的上表面距离地面高H=5m,子弹穿过纸筒的过程中所受的摩擦力和空气阻力忽略不计,取g=10m/s2。求: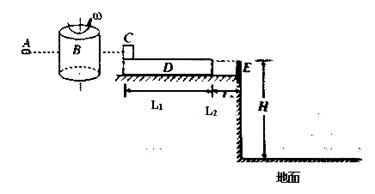

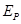 ;
; 、
、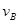 大小.
大小.
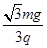 .先把杆拉成水平,然后将杆无初速释放,重力加速度为g,不计空气阻力,则( )
.先把杆拉成水平,然后将杆无初速释放,重力加速度为g,不计空气阻力,则( )
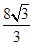 mg
mg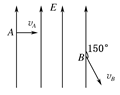
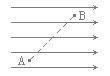
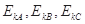 ,则它们间的关系应是( )
,则它们间的关系应是( )
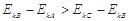 B.
B.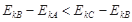
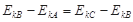 D.EKC>2EKB
D.EKC>2EKB