题目内容
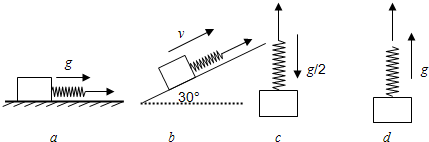
如图所示，四根相同的轻弹簧连接着相同的物体，在外力作用下做不同的运动（不计摩擦和空气阻力）．设四根轻弹簧的伸长量分别为△l甲、△l乙、△l丙、△l丁，下列关系正确的是（ ）
分析：分别根据牛顿第二定律、平衡条件求出弹簧的弹力，由胡克定律判断四根弹簧伸长量的大小．
解答：解：
（1）根据牛顿第二定律和胡克定律得：k△l甲=ma=mg，得△l甲=
（2）由平衡条件和胡克定律得：k△l乙=mgsinθ，得△l乙=
sin30°=0.5
（3）由平衡条件和胡克定律得：k△l丙=mg，得△l丙=
（4）根据牛顿第二定律和胡克定律得：k△l丁-mg=mg，得△l丁=2
所以△l甲＞△l乙，△l丙＜△l丁，△l甲＜△l丁，△l乙＜△l丙＜△l丁
故选：ABC．
（1）根据牛顿第二定律和胡克定律得：k△l甲=ma=mg，得△l甲=
| mg |
| k |
（2）由平衡条件和胡克定律得：k△l乙=mgsinθ，得△l乙=
| mg |
| k |
| mg |
| k |
（3）由平衡条件和胡克定律得：k△l丙=mg，得△l丙=
| mg |
| k |
（4）根据牛顿第二定律和胡克定律得：k△l丁-mg=mg，得△l丁=2
| mg |
| k |
所以△l甲＞△l乙，△l丙＜△l丁，△l甲＜△l丁，△l乙＜△l丙＜△l丁
故选：ABC．
点评：本题是牛顿第二定律、平衡条件和胡克定律的综合应用，比较简单．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
如图所示，四根相同的轻质弹簧连着相同的物体，在外力作用下做不同的运动：
如图所示，四根相同的弹簧都处于水平位置，右端都受到大小皆为F的拉力作用，而左端的情况各不相同：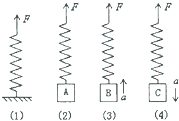
如图所示，四根相同的轻质弹簧都处于竖直状态，上端都受到大小皆为F的拉力作用，针对以下四种情况：