题目内容
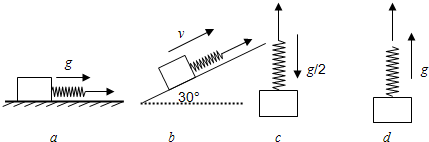
 如图所示,四根相同的轻质弹簧连着相同的物体,在外力作用下做不同的运动:
如图所示,四根相同的轻质弹簧连着相同的物体,在外力作用下做不同的运动:①在光滑水平面上做加速度大小为g的匀加速直线运动;
②沿光滑斜面做匀速直线运动;
③做竖直向下的匀速直线运动,
④做竖直向上的加速度大小为g的匀加速直线运动.
设四根弹簧伸长量分别为△l1、△l2、△l3、△l4,不计空气阻力,g为重力加速度,则( )
分析:如图,根据物体的运动情况,进行受力分析,因为水平面和斜面都是光滑的,所以不考虑摩擦力,同样的弹簧,则倔强系数K相同,根据胡可定律,F=K△l,则不同的弹簧拉力就有不同的伸长量,逐个分析,即可得解.
解答:解:①物体竖直方向受到一对平衡力重力和支持力,水平方向受到弹簧弹力F=K△l1,使物体做加速度大小为g的匀加速直线运动,根据牛顿第二定律, F=mg=K△l1,则△l1=
F=mg=K△l1,则△l1=
;
②物体受重力,分解为垂直斜面的分力mgcosθ和斜面对物体的支持力构成一对平衡力,和斜面沿斜面向下的分力mgsinθ与弹簧的拉力F=K△l2构成一对平衡力,所以mgsinθ=K△l2,则△l2=
;
③物体受到重力mg和弹簧的拉力K△l3,构成一对平衡力,所以mg=K△l3,则△l3=
;
④物体受到重力mg和弹簧的拉力K△l4,做向上的匀加速运动,由牛顿第二定律,得F-mg=mg,所以F=K△l4=2mg,
则△l4=
;
因为
>
>
,
所以△l4>△l1=△l3>△l2;
故选:A.
 F=mg=K△l1,则△l1=
F=mg=K△l1,则△l1=| mg |
| K |
②物体受重力,分解为垂直斜面的分力mgcosθ和斜面对物体的支持力构成一对平衡力,和斜面沿斜面向下的分力mgsinθ与弹簧的拉力F=K△l2构成一对平衡力,所以mgsinθ=K△l2,则△l2=
| mgsinθ |
| K |
③物体受到重力mg和弹簧的拉力K△l3,构成一对平衡力,所以mg=K△l3,则△l3=
| mg |
| K |
④物体受到重力mg和弹簧的拉力K△l4,做向上的匀加速运动,由牛顿第二定律,得F-mg=mg,所以F=K△l4=2mg,
则△l4=
| 2mg |
| K |
因为
| 2mg |
| K |
| mg |
| K |
| mgsinθ |
| K |
所以△l4>△l1=△l3>△l2;
故选:A.
点评:认真分析题意,把物体进行受力分析,再根据物体的运动情况,利用受力平衡或牛顿第二定律列出等式是解决此题的关键.

练习册系列答案
相关题目

 如图所示,四根相同的弹簧都处于水平位置,右端都受到大小皆为F的拉力作用,而左端的情况各不相同:
如图所示,四根相同的弹簧都处于水平位置,右端都受到大小皆为F的拉力作用,而左端的情况各不相同: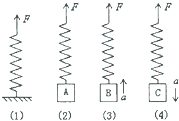 如图所示,四根相同的轻质弹簧都处于竖直状态,上端都受到大小皆为F的拉力作用,针对以下四种情况:
如图所示,四根相同的轻质弹簧都处于竖直状态,上端都受到大小皆为F的拉力作用,针对以下四种情况: